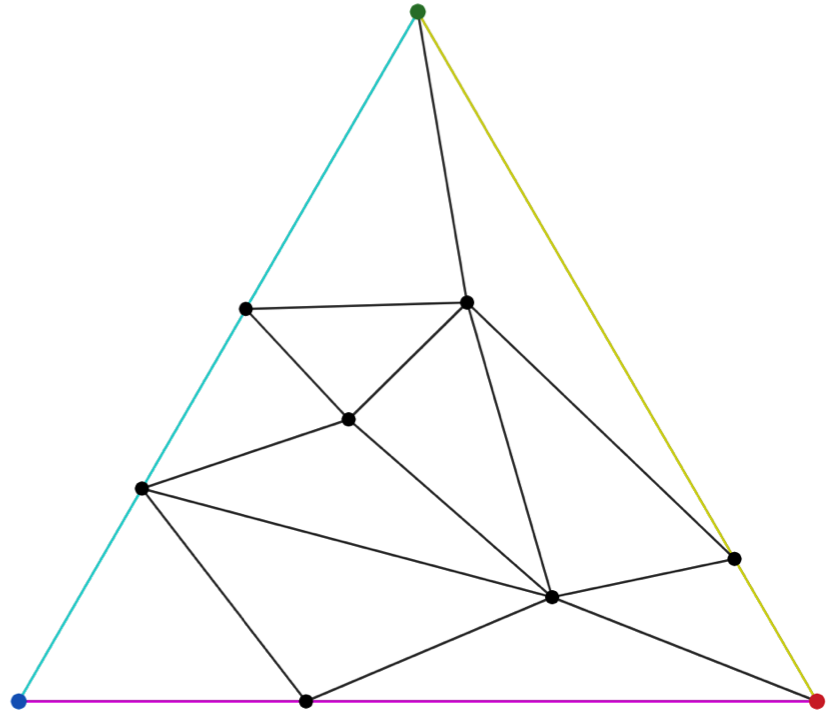
Adriana y Belén están jugando con una hoja de papel, una pluma negra y seis colores distintos. Lo primero que hacen es dibujar el tablero, el cual es un triángulo que tiene cada uno de sus vértices y aristas coloreados con un color distinto. A continuación ambas colocan puntos negros sobre las aristas del triángulo y dentro del triángulo, finalmente, van uniendo todos los puntos con aristas de tal manera que forman muchos triangulitos dentro, como lo muestra la siguiente imagen:
Las reglas del juego son las siguientes: El juego es de turno por turno, el primer jugador hace una jugada y luego el segundo jugador hace su movimiento.
El movimiento de cada jugador consiste en colorear un punto negro con alguno de los colores de los vértices del triángulo inicial bajo la restricción de que los puntos negros sobre las aristas de colores sólo pueden ser coloreados con el color de los vértices de esas aristas. Por ejemplo, en la imagen anterior: los puntos negros sobre la arista de color cian pueden ser coloreados tanto de azul como verde, o el punto negro que está sobre la arista magenta puede ser coloreado por azul o rojo. El resto de puntos negros que no están sobre alguna de las aristas coloreadas, puede ser de cualquiera de los 3 colores de los vértices del triángulo.
Si al colorear un punto negro formas un triangulito que tiene sus tres vértices con distintos colores, entonces anotas la inicial de tu nombre dentro del triangulito y gana el jugador que forme la menor cantidad de este tipo de triangulitos. El juego termina cuando ya no quedan puntos negros por colorear.
En las siguientes imágenes se muestra el desarrollo del primer juego que tuvieron Adriana y Belén.
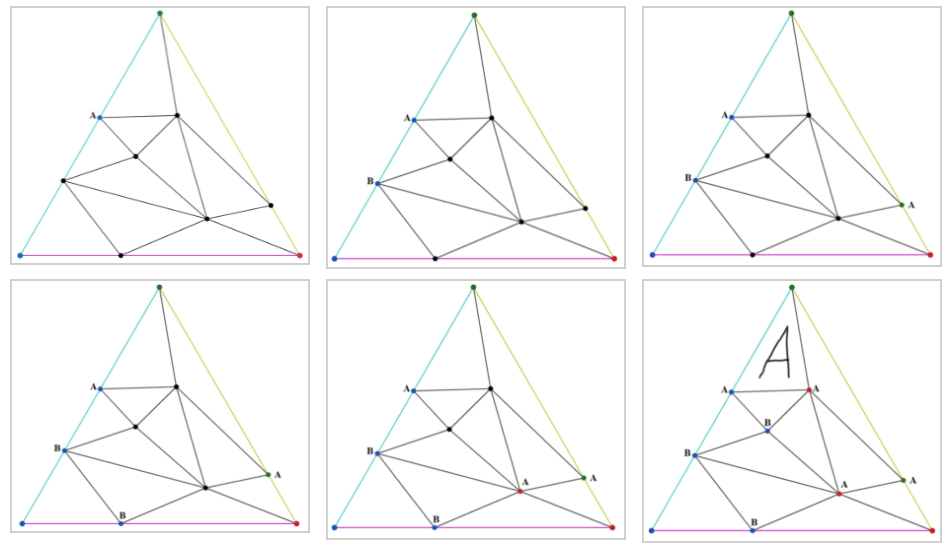
Adriana, enojada por haber perdido, le pidió una revancha a Belén y volvió a perder. Adriana le pidió otra revancha pero perdió otra vez. Belén le dijo a Adriana que ella no iba a ser capaz de ganar ni una sola vez y Adriana le respondió que por lo menos conseguiría el empate. Ambas continuaron jugando, pero Adriana siempre perdió y nunca consiguió el empate; sonó el timbre del recreo y ambas regresaron a sus salones de clases.
Lo anterior suena a un cuento sobre niños jugando ¿verdad? ¿Qué pensarías si te dijeran que ese juego tiene matemáticas muy complejas detrás?
Algo impresionante sobre el juego anterior es que jamás puede terminar en empate, eso significa que siempre vas a formar una cantidad impar de triangulitos con cada vértice de distinto color. Al resultado anterior se le conoce como Lema de Sperner, pues fue Emanuel Sperner, matemático alemán, quien demostró en 1928 que en ese juego nunca hay empates. El Lema de Sperner es un resultado fascinante no sólo porque puede explicarse como un juego, sino porque es increíblemente útil.
Supón que tres amigos quieren rentar un departamento con tres habitaciones, todas en buenas condiciones; sin embargo, puede que alguna sea la más grande o alguna esté más cerca del baño, por lo que los tres amigos debaten sobre cuánto deberían pagar por la habitación que quieren.
El Lema de Sperner nos ayuda a decidir qué amigo debe quedarse con cuál habitación y por cuánto dinero, de tal manera, que cada uno quede contento con la habitación que le tocó y con cuánto dinero tiene que pagar por ella. A este tipo de problemas se les llama comúnmente como problemas de divisiones justas, libres de envidia y los economistas se enfrentan a ellos.
También es útil para los mismos matemáticos, pues les ayuda a demostrar Teoremas. El Teorema más conocido probablemente sea el Teorema de Pitágoras al cual todos los estudiantes de secundaria deben enfrentarse.
Los Teoremas son afirmaciones que, a través de argumentos, han sido verificados como verdaderos y el trabajo de los matemáticos es justamente verificar afirmaciones para convertirlas en Teoremas, a estas verificaciones les llaman demostraciones.
Un teorema fascinante es el Teorema del punto fijo de Brouwer, el cual resulta ser sumamente complicado y pertenece a una rama de las matemáticas llamada topología algebraica. Se necesita estudiar mucha teoría matemática de nivel universitario para comprender lo que dice el teorema y se necesita mucha más teoría para lograr demostrarlo como lo hizo Luitzen Egbertus Jan Brouwer, matemático neerlandés en 1912. Sin embargo, Emanuel Sperner le mostró al mundo que uno no debía ser experto en topología algebraica para poder demostrarlo, bastaba con entender su lema para poder demostrarlo con facilidad.
Y a todo esto ¿qué dice el Teorema del punto fijo de Brouwer? ¿Qué pensarías si te dijeran que es probable que te encuentres con él cuando comes?
EL TEOREMA DEL PUNTO FIJO DE BOUWER
Si has comido caldo de pollo probablemente has observado que en la superficie del caldo se forman burbujas de grasa y probablemente has agitado tu caldo para moverlas. El Teorema del punto fijo de Brouwer implica que sin importar cómo agites tu caldo con tu cuchara, siempre existirá una pequeña burbujita que va a quedar en el mismo lugar que estaba justo antes de que empezaras a agitar.
Nótese que a pesar de que podemos ejemplificarlo, sigue resultando un Teorema complicado y abstracto, porque no nos dice cuál burbuja va a ser la que queda intacta, sólo nos dice que existirá una de ellas.
El Lema de Sperner tiene tantas aplicaciones que simplemente no podríamos escribirlas todas en un sólo artículo, por eso la próxima vez que veas a alguien jugar algún juego o tú mismo juegues un juego piensa que quizá ese juego tenga algún Teorema por ahí escondido.