El 23 de octubre de 1852, Augustus de Morgan, profesor de matemáticas en la Universidad de Londres, escribió una carta a su colega y amigo sir William Rowan Hamilton, distinguido matemático y físico irlandés. Tanto De Morgan como Hamilton son personajes importantes en el desarrollo de las ciencias exactas. De Morgan hizo notables contribuciones a la lógica matemática, mientras que Hamilton también realizó diversas aportaciones, siendo la teoría de los cuaterniones la más emblemática.
Detengámonos a pensar cómo era el mundo, en particular el mundo de las comunicaciones, a finales del siglo XIX. El acceso a la información y al conocimiento, así como la colaboración entre comunidades científicas de diferentes países, se encontraban en pañales. No creo que nadie hubiera soñado nada cercano a lo que tenemos ahora, nada cercano al internet o a la World Wide Web.
Los aportes científicos en todas las ramas del conocimiento tardaban mucho en darse a conocer, pudiendo pasar semanas o meses en llegar de un punto del planeta a otro. De modo que muchas veces la correspondencia epistolar entre colegas era la más eficiente manera de mantenerse al tanto de las novedades. En otras palabras, cuando alguien tenía una pregunta o curiosidad acerca de algo, en vez de googlearlo, lo que se hacía era escribir una carta a quien se pensara más capaz de contestar. La correspondencia entre De Morgan y Hamilton fue constante y nutrida en ese sentido.
Imagino a De Morgan caminando a su casa, después de un largo día en la universidad, sin prestar atención a la llovizna o a los carruajes, reflexionando acerca de lo que le había dicho aquel joven entre clases. Imagino cómo llega a su hogar, se quita el oscuro abrigo, limpia el cristal de sus quevedos, e ignorando la presencia de Sophia Elizabeth y de los niños se encierra en su estudio como de costumbre. Entonces, sin sospechar la trascendencia que tendría lo que estaba a punto de escribir, busca la pluma y el tintero; abre el cajón, selecciona cuatro hojas y a la luz de las velas comienza:
Mi querido Hamilton:
El día de hoy, uno de mis alumnos me pidió que le diera la razón de ser de un hecho que yo no sabía que era un hecho, y aún no lo sé. Él afirma que si una figura está dividida de cualquier manera, y sus compartimentos son coloreados de modo tal que aquellas partes con alguna porción de línea frontera en común reciben diferente color, quizá se requieran cuatro colores, pero no más. El siguiente es un caso en el cual se requieren cuatro colores. La cuestión es si no se puede inventar uno que necesite cinco… ¿Qué me puedes decir al respecto? Y, si esto es verdad, ¿crees que se había notado ya antes? Mi pupilo dice que lo descubrió coloreando un mapa de Inglaterra… Mientras más lo pienso, más evidente me parece. Si me contestaras con un ejemplo sencillo que me hiciera ver como un animal estúpido, creo que tendría que hacer lo que La Esfinge hizo…

Con respecto a “hacer lo que La Esfinge hizo” se refería a terminar su existencia lanzándose al vacío desde un acantilado, como cuenta la mitología que La Esfinge hizo, después de que Edipo la venciera. Lo que transmite De Morgan es una sensación de frustración desesperada al no poder contestar una pregunta tan fácil, aun con el convencimiento de la respuesta. En su defensa, él no podía saber cuánto tiempo pasaría antes de que alguien en el mundo pudiera hacerlo.
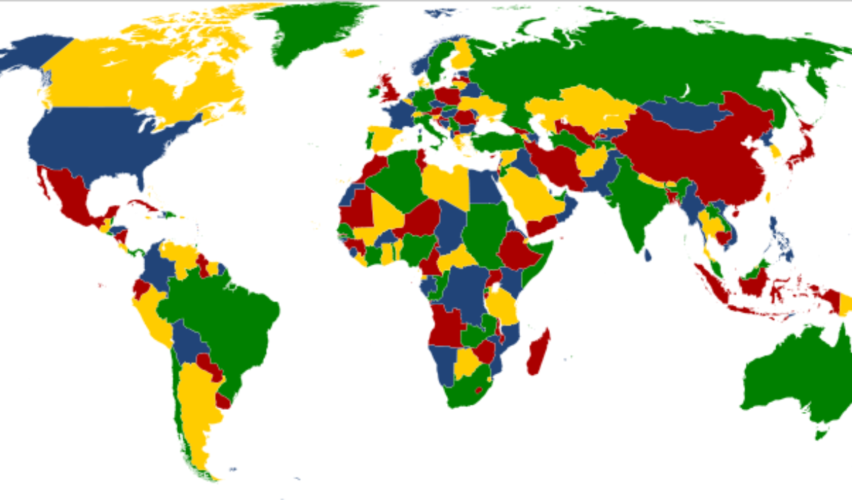
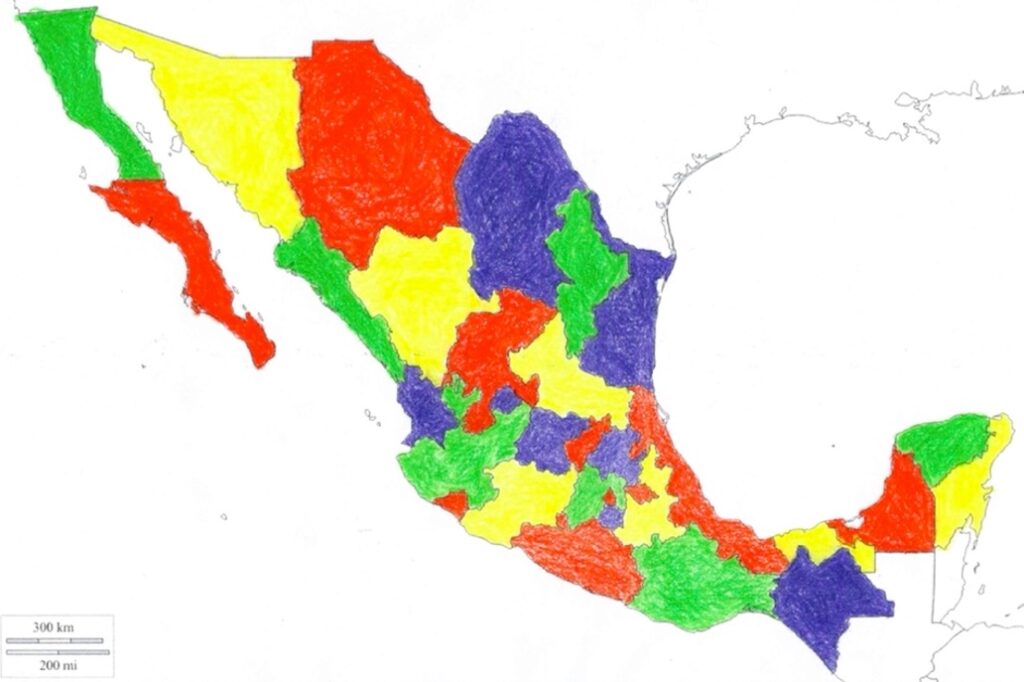
El problema que describe De Morgan a Hamilton en la famosa carta es conocido como “el problema de los cuatro colores”. Dicho problema establece simplemente que cualquier mapa, real o imaginario, se puede “colorear propiamente” con a lo más cuatro colores. El significado de “colorear propiamente” se refiere a asignar un color a cada región del mapa de modo que correspondan colores distintos a regiones vecinas. Por ejemplo, véase el siguiente mapa de la República Mexicana:
Se sabe que Hamilton contestó escuetamente a la carta de De Morgan:
No creo que pueda intentar resolver tu “cuaternio de colores” prontamente.
No hay evidencias de que Hamilton y De Morgan hayan tocado el tema nuevamente. El alumno que abordó a De Morgan en 1852 fue Frederick Guthrie, quien posteriormente se convertiría en un físico de renombre, fundador de la Sociedad de Física en Londres.
Más tarde se supo que no fue él quien, coloreando un mapa de Inglaterra, se planteó por primera vez el problema de los cuatro colores. Fue su hermano Francis, como el propio Frederic lo explica en otra carta. Quizás más personas, antes y después de Francis, se hayan planteado la misma pregunta al colorear algún mapa. La carta de De Morgan a Hamilton es el documento conocido más antiguo en el que se hace referencia al problema de los cuatro colores.
De Morgan murió en 1871 sin saber la solución de dicho problema; es decir, nunca supo la respuesta a la pregunta que le planteó a Hamiton en esa carta: nunca supo si es verdad o no que cualquier mapa se pueda colorear propiamente con a lo más cuatro colores. De Morgan murió con la duda de que tal vez existiera un mapa que requiere cinco colores para ser coloreado sin que regiones vecinas tengan el mismo color.
La historia de la resolución del problema de los cuatro colores es larga e intrincada. Abarca desde 1852, con la historia de la carta que he referido, hasta 1977, cuando en el Illinois Journal of Mathematics apareció publicada la prueba del teorema de los cuatro colores, en dos extensos artículos y un enorme suplemento.
En el medio de la historia, aparecen diferentes personajes, ensayos, pruebas y errores. Finalmente, la prueba del teorema de los cuatro colores es una prueba asistida por computadora. Appel, Haken y Koch, quienes fueron los autores de dichos artículos, utilizaron más de mil horas de tiempo computacional en una IBM-360. Actualmente, no se conoce una prueba sustancialmente mejor que esa.
Así como el teorema de los cuatro colores, existen en diversas áreas de las matemáticas enunciados sospechosamente simples que no podemos probar; o que si podemos lo hacemos de maneras absolutamente complejas. ¿Cómo es posible que enunciados tan sencillos demanden pruebas tan largas y complicadas?