El pintor alemán Paul Klee (1879-1940) dijo que “una línea es un punto que fue a dar un paseo”, yo agregaría que el punto eligió una dirección y decidió no regresar. En el caso del círculo, podemos decir que el punto se fue de paseo y regresó a casa, ya que hace un curva que se conoce como cerrada. Pero, el círculo es una curva cerrada con una propiedad muy particular, tiene ancho constante.
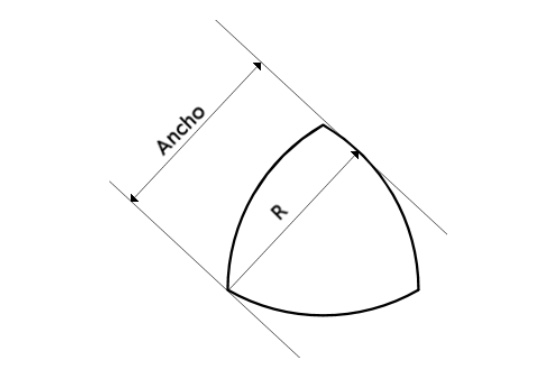
Vamos a definir lo que significa que una curva tenga ancho constante. Toma dos tangentes paralelas a una curva cerrada, la distancia entre estas dos líneas es el ancho de la curva respecto a estas tangentes. Decimos que una curva tiene ancho constante si el ancho es idéntico independientemente de la dirección que tomen las tangentes. Si tenemos una curva de ancho constante, podemos encerrar la curva dentro de un cuadrado y sin importar cuánto la giremos siempre estará en contacto con los cuatro lados del cuadrado.
Existen otras curvas, distintas del círculo, que sorprendentemente son de ancho constante. Una de ellas se conoce como el triángulo de Reuleaux, pues fue idea del ingeniero alemán F. Reuleaux (1829-1905). Esta figura de ancho constante ha tenido distintas aplicaciones en la ingeniería y la arquitectura. Por ejemplo, el triángulo de Reuleaux es parte del mecanismo utilizado en muchos de los antiguos proyectores de cine para evitar que la imagen se viera borrosa [2].
Sabemos que para dibujar un círculo requerimos de un compás. Simplemente colocamos la aguja en el punto que será el centro y giramos el compás para que la punta de grafito dibuje el círculo. También podemos usar un compás para dibujar un triángulo de Reuleaux:
1. Abre el compás con el radio que prefieras y dibuja un círculo.
2. Coloca la punta de la aguja en cualquier punto del círculo que acabas de dibujar y traza otro círculo del mismo radio con centro allí.
3. Ahora coloca la punta de la aguja en uno de los dos puntos en donde se cruzan estos círculos y dibuja un tercer círculo.
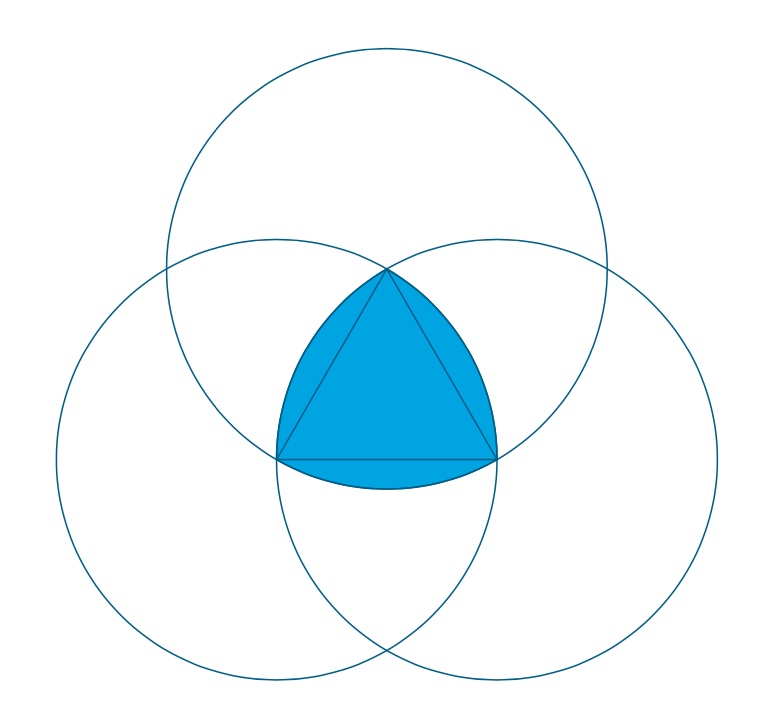
Encontrarás que, al centro de tu dibujo, hay una figura similar a un “triángulo redondeado”, esta figura es el triángulo de Reuleaux. Como acabas de verificar, la construcción del triángulo de Reuleaux es muy sencilla. Observa que, conectando todos los vértices del triángulo de Reuleaux se obtiene un triángulo equilátero.
Sabemos que la esfera es la versión tridimensional del círculo, y justamente la esfera es un cuerpo de ancho constante. Podemos decir que un objeto tridimensional es de ancho constante si podemos guardarlo dentro de un cubo de tal manera que, sin importar cuánto lo giremos, siempre estará en contacto con las seis caras del cubo.
Construir cuerpos de ancho constante no es tan sencillo. Si reproducimos la construcción del triángulo de Reuleaux usando esferas y un tetraedro regular, el objeto que se obtiene es conocido como tetraedro de Reuleaux, que puede pensarse como un tetraedro “inflado”, sin embargo, no es de ancho constante.
En 1911, Meissner mostró cómo modificar el tetraedro de Reuleaux [2] para obtener un cuerpo de ancho constante reemplazando tres de sus bordes con “parches” formados al rotar un arco circular. Los “parches” deben tener un vértice común o formar un triángulo.
Además de los cuerpos de Meissner, se conocen pocas construcciones de cuerpos de ancho constante en dimensión tres. En marzo de 2022, conjuntamente con la Dra. Déborah Oliveros y el Dr. Luis Montejano, de la Unidad Juriquilla del Instituto de Matemáticas, publicamos la construcción de una nueva familia de cuerpos de ancho constante, inspirados en una construcción propuesta por P. Roberts en 2011 [3].
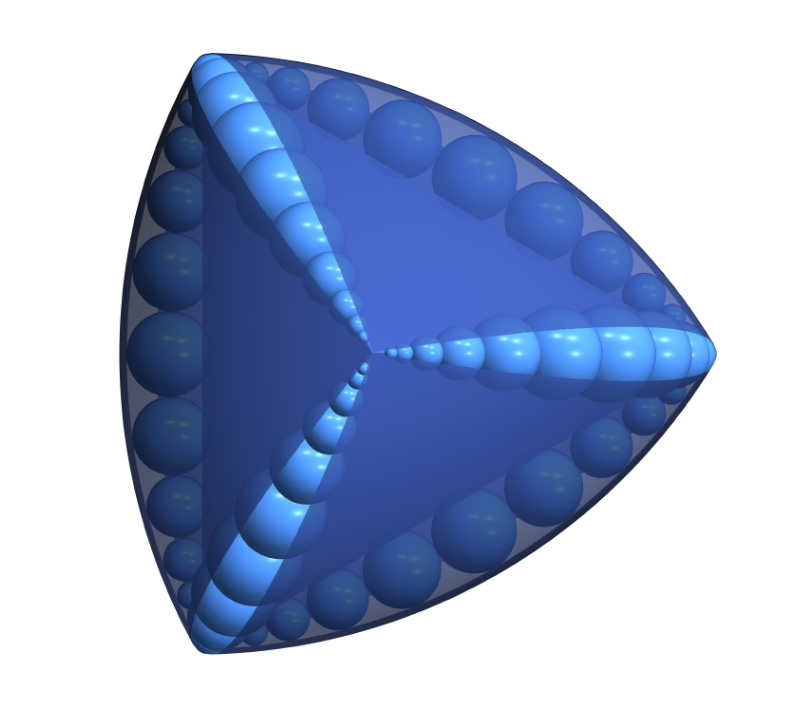
La construcción consiste en reemplazar cada uno de los seis bordes del tetraedro de Reuleaux con una “envoltura de esferas” [1]. Cada envoltura consiste de esferas tangentes a una arista del tetraedro y, al mismo tiempo, tangentes a las caras esféricas del tetraedro de Reuleaux. Hemos llamado a esta colección de cuerpos de ancho constante “cuerpos chícharo”. Si las seis envolturas son iguales, el cuerpo obtenido tiene la misma simetría del tetraedro.
Referencias
[1] Arelio, I., Montejano, L., Oliveros, D. Peabodies of constant width. Beitr Algebra Geom (2022). https://doi.org/10.1007/s13366-022-00637-z
[2] Martini, H., Montejano, L., Oliveros, D. Bodies of Constant Width: An Introduction to Convex Geometry With Applications. Birkha ̈user, Boston, Bassel, Stuttgart, 2019.
[3] Roberts, Patrick. Spheroform with Tetrahedral Symmetry, http://www.xtalgrafix.com/Spheroform2.htm
El doctor Isaac Arelio Ríos es investigador de la Unidad Académica del Instituto de Matemáticas de la Universidad Nacional Autónoma de México
AQUÍ PUEDES LEER TODAS LAS ENTREGAS DE “DESDE LA UNAM”, LA COLUMNA DE LA UNAM CAMPUS JURIQUILLA PARA LALUPA.MX
https://lalupa.mx/category/aula-magna/desde-la-unam/