Los mosaicos nos acompañan en nuestra vida todo el tiempo; en el baño, en la cocina y prácticamente en todos lados. Los más sencillos están formados por polígonos regulares del mismo tipo, por ejemplo, cuadrados, hexágonos regulares o triángulos equiláteros etc., pero también se pueden formar mosaicos combinando varios tipos de polígonos y diseños muy peculiares.
A lo largo de la historia, distintas culturas han creado hermosos diseños de mosaicos con diversos motivos. Ejemplos de estos los podemos encontrar en los mosaicos griegos, como los provenientes de la isla de Delos, que datan de la última mitad del siglo II a. C. y principios del siglo I a. C. Los mosaicos romanos fueron utilizados como elementos decorativos en la arquitectura, y estos llegaron a ser un arte muy apreciado que puede encontrarse prácticamente en todo lo que abarcó el Imperio romano. El mosaico cristiano aportó la novedad de utilizarse para decorar paredes y bóvedas de iglesias, pero desafortunadamente, con la caída del Imperio romano de occidente, los mosaicos fueron perdiendo terreno, excepto en Italia y en el mundo bizantino. El mosaico árabe es también una prueba fantástica de despliegue de belleza y composición, con un alto contenido geométrico. La religión islámica prohíbe la representación de figuras de la naturaleza, por tal motivo sus manifestaciones artísticas buscan la belleza en los diseños geométricos abstractos. De hecho, se cree que los encargados de la composición de los mosaicos eran los matemáticos, y que utilizaban regla y compás para elaborar los patrones. El arte de llenar el plano con repeticiones de figuras alcanzó su máxima expresión en la España musulmana, durante el siglo XIII, y en la Alhambra de Granada se encuentran varios de estos ejemplos maravillosos (Ver figura 1 izquierda). Vale la pena mencionar también los magníficos mosaicos y frisos que se encuentran en sitios arqueológicos en México, como en Mitla, Oaxaca.

En épocas modernas existen también varios ejemplos de diseños sorprendentes, como aquellos diseñados por el artista M. C. Escher (1898-1972) (ver figura 1 derecha), quien probablemente obtuvo inspiración de sus viajes a la ciudad de Granada; de hecho, su técnica es muy similar a la utilizada en los mosaicos de la Alhambra. Partiendo de una figura geométrica muy sencilla, él aplicaba transformaciones como giros, traslaciones y deslizamientos sucesivos, hasta llegar a la construcción de un motivo que rellena todo plano.
En matemáticas, los mosaicos son, grosso modo, el recubrimiento (infinito) del plano mediante figuras, de tal forma que no se solapen ni queden huecos entre ellas, y las piezas que se utilizan reciben el nombre de teselas o losetas. El término tesela proviene del latín tessellam, o pieza de mármol, piedra etc.
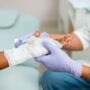
Se dice que un mosaico es periódico cuando podemos delimitar en él una región que, mediante una traslación o desplazamiento, se repite. Es decir, con un solo sector del plano tenemos la regla para ampliar este patrón y extenderlo infinitamente hasta recubrir todo el plano o, dicho de otra manera, podemos encontrar el patrón de cómo está hecho el mosaico trasladándonos de un punto a otro. El mosaico de Escher en la figura 1 es un buen ejemplo de un mosaico periódico. Hay muchas formas de crear mosaicos no periódicos, de hecho, es relativamente sencillo convertir una tesela periódica en una no periódica; por ejemplo, alterando las orientaciones de las teselas, con el fin de evitar la periodicidad. En la siguiente figura, el triángulo azul es la tesela que da lugar a un mosaico del plano; en el ejemplo de la izquierda se puede ver fácilmente que esta genera una teselación periódica, en la cual el patrón se repite por traslaciones, pero en el lado derecho el arreglo da lugar a una teselación que es no periódica, pues no existe manera de que coincida alguna región del plano con otras y se repita el patrón.
En el año 1960 el matemático Hao Wang se preguntó si existía algún conjunto de losetas aperiódicas, es decir, si habría un conjunto de piezas o losetas específicas con las que al producir un mosaico siempre resulte de tipo no periódico. Además, Wang relacionó este problema con uno de los teoremas fundamentales de la matemática y la informática teórica, conocido como teorema de indecidibilidad de Gödel. Wang conjeturó que no existían conjuntos de losetas aperiódicas, es decir, estaba convencido de que en cualquier conjunto de losetas que cubriera el plano habría siempre una manera de acomodarlas para que el mosaico resultante fuera periódico.
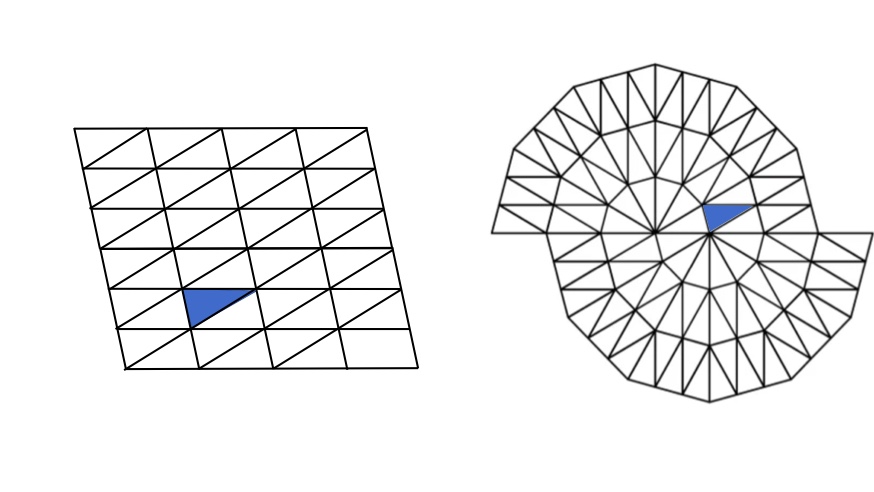
En 1966, el matemático Robert Berger, estudiante de Wang, construyó un ejemplo que contenía 20,426 losetas y es aperiódico. Este ejemplo dio lugar entonces a la siguiente pregunta: ¿Cuál será el conjunto mínimo de losetas que es aperiódico? Durante décadas, matemáticos profesionales y amateurs se dedicaron a buscar ejemplos de conjuntos aperiódicos. De hecho, el propio Berger consiguió reducir el tamaño de su conjunto hasta encontrar una colección de 104 losetas aperiódicas. En 1968, Knuth encontró otro conjunto con 92, y en 1971 Robinson dio uno con sólo seis losetas aperiódicas. Finalmente, en 1978 aparece el famoso mosaico de Penrose, que consiste en sólo dos losetas “el dardo y el cometa” (ver la figura 3 del lado izquierdo). El museo Universum, ubicado en la Ciudad Universitaria de la UNAM, tiene un hermoso ejemplo del mosaico de Penrose echo por artesanos mexicanos, vale mucho la pena verlo.
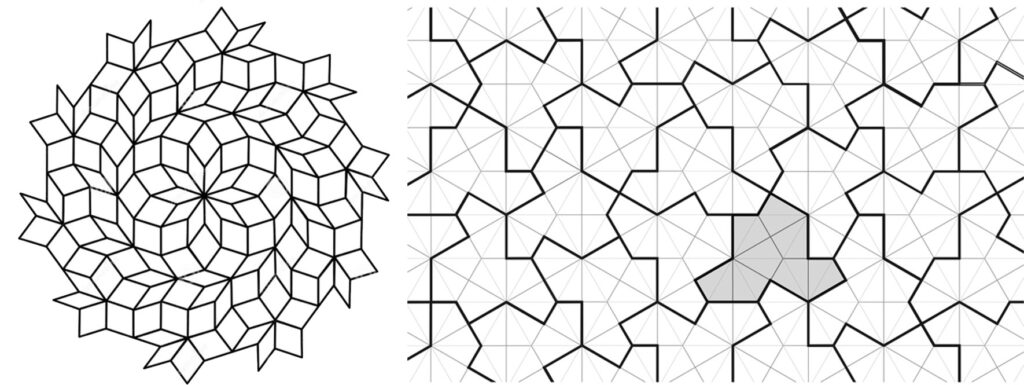
Obviamente, la pregunta de si se puede reducir este conjunto de dos a una sola loseta que recubra el espacio de manera infinita, sin dejar espacios, y que resulte en un mosaico aperiódico estuvo en el aire desde entonces. El 20 de marzo de este año, un grupo de matemáticos estadounidenses y canadienses, conformado por David Smith, Joseph Samuel Myers, Craig S. Kaplan y Chaim Goodman-Strauss, publicaron un ejemplo de loseta aperiódica (ver figura 3 a la derecha); noticia que a todos los matemáticos en el mundo nos tiene muy entusiasmados, no sólo porque resuelve una pregunta abierta por más de 50 años, sino porque, además, tiene implicaciones interesantes en la informática teórica.
La doctora Déborah Oliveros Braniff es investigadora en la Unidad Juriquilla del Instituto de Matemáticas de la UNAM
AQUÍ PUEDES LEER TODAS LAS ENTREGAS DE “DESDE LA UNAM”, LA COLUMNA DE LA UNAM CAMPUS JURIQUILLA PARA LALUPA.MX
https://lalupa.mx/category/aula-magna/desde-la-unam/