Las matemáticas tienen un rol importante en la vida cotidiana y en nuestra sociedad. El objetivo de la enseñanza de las matemáticas es alcanzar la capacidad de identificar y entender cuál es su función en nuestro día a día (Baleño, 2022; Domínguez-Morales et al., 2022).
A través de las matemáticas podemos construir, ver, organizar, realizar y tomar decisiones de forma autónoma. Incluso se vuelven un factor importante al momento de decidir una carrera. De acuerdo con Macías-González et al. (2019), un estudio realizado a 437 estudiantes de dos instituciones educativas mostró que sólo el 1.37 % tuvo interés en estudiar física, matemáticas y ciencias de la Tierra.
De acuerdo con la Comisión Nacional para la Mejora Continua de la Educación (2020), el puntaje en matemáticas de los estudiantes mexicanos se ubica entre 358 y 420 puntos, con un promedio de 409 puntos y una desviación de 84.
El pensamiento matemático (PM) tiene poca presencia en las aulas. Muchas veces solemos enseñar matemáticas en formas técnicas y de conceptos, omitiendo la solución de problemas. Por esta razón, algunos expertos señalan que las matemáticas no llegan a ser útiles en la vida del estudiante ni trascienden en el círculo en el que se desenvuelven. Pero, ¿qué es PM? Podemos definir PM como el conjunto de operaciones, procedimientos, algoritmos y hasta procesos mentales utilizados para la solución de problemas, así como la utilización y creación de modelos.
El PM es de gran utilidad fuera de la escuela, por ejemplo, al tomar decisiones. A través del PM podemos comprender las leyes de la ciencia que utilizan a las matemáticas para expresarse. Nos permite explicar fenómenos del mundo real, incluso resolver problemas de otras áreas.
Las cuatro categorías que abarca el PM son:
- Procedural.
- Procesos de razonamiento.
- Solución de problemas y modelación.
- Interacción y lenguaje matemático.
Dentro de la tercera categoría encontramos las siguientes subcategorías:
- Uso de modelos.
- Construcción de modelos.
- Estrategias heurísticas y ejecución de procedimientos no rutinarios.
Particularmente, en este texto abordaremos el uso, importancia y construcción de modelos.
¿Te imaginas el PM en la música, el juego, el deporte, redes sociales, moda, transporte y construcción? Te invito a reflexionar con algunos ejemplos.

Es 2018 y en Rusia se está disputando la Copa Mundial FIFA. Lionel Messi se enfrenta a Hannes Halldórsson en un penal al minuto 63. Messi mira fijamente el balón, se prepara a tirar, toma carrera y sorprendentemente lo falla. El público ovaciona a Halldórsson por haber atajado el penal, ¿cómo fue esto posible?, ¿qué hizo Messi para fallarlo?, ¿cómo pudo el arquero atajarlo?, ¿es posible que el PM nos ayude a encontrar la respuesta a estas preguntas? La respuesta es sí.
Lopes et al. en 2014 realizaron un estudio para encontrar la relación entre la dirección del tiro y aspectos de los movimientos de los jugadores en sus condiciones de espacio y tiempo al momento de tirar penales. Para su trabajo, los autores no sólo utilizaron estadística, sino también modelos para encontrar relaciones entre el ángulo del pie, rodilla, cadera, hombro, así como el movimiento del pie y la velocidad de disparo. Gracias a la construcción y uso de modelos, pudieron encontrar que, a pesar de que el tirador intente engañar al arquero, los momentos finales antes del contacto con el balón le proporcionan al portero información de la dirección hacia donde podría ir el balón.
En el mismo contexto, el balón de futbol se ha visto en la necesidad de evolucionar a lo largo de 90 años. ¿El objetivo? mejorar su aerodinámica, rebote y ligereza, así como su deslizamiento en el pasto (Guzmán, 2022). En palabras de los fanáticos del futbol: “tener goles espectaculares con efectos de otra dimensión”. Entonces, ¿puede el PM ayudarnos a alcanzar este objetivo? Escalante y Pacheco (2005) encontraron que esto era posible a partir de un modelo matemático. Con su trabajo, encontraron una distribución de paneles adecuada en el diseño de un balón de futbol a partir de un diseño inicial.
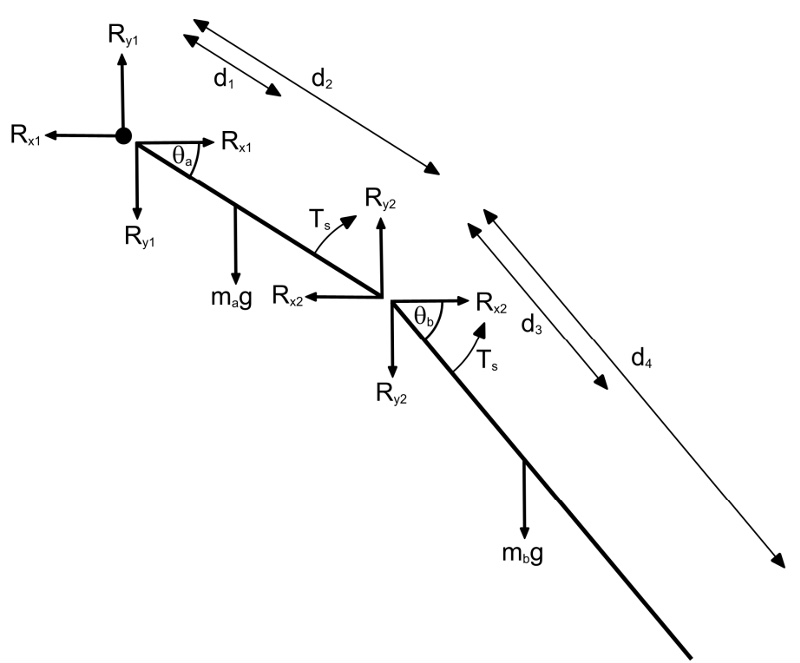
¿En qué otros deportes podemos encontrar el pensamiento matemático? Como nos comentan Herrera-Aguilar et al., (2019) está presente en el tiro parabólico que forma la salida de los competidores en natación, en la representación de diagramas de cuerpo libre de los gimnastas en el trampolín olímpico, salto de caballo, o bien en el balanceo de un gimnasta alrededor de una barra alta (ver Figura 2).
Siguiendo con ejemplos en los deportes, ¿puede cualquier persona practicar ciclismo?, para hacerlo, ¿se necesita de una bicicleta especial? El trabajo de Blocken et al. (2018) nos ha ayudado a entender que la posición del ciclista, los ángulos de varias partes del cuerpo, como el hombro, codo, antebrazo, incluso la rodilla, son factores que influyen en el desempeño de los ciclistas en un concurso contrarreloj por equipos (TTT).
Ahora que vivimos una pandemia, ¿cómo fue que gobiernos locales y organizaciones de salud tomaron decisiones para tratar de reducir el contagio? La respuesta de nueva cuenta es, sí, gracias al pensamiento matemático. A través de modelos que nos ayudaban a entender cómo es que el virus se propagaba, en qué condiciones y qué factores influyen (de León et al., 2020; Acuña-Zegarra, et al., 2020; Ramírez-Valverde & Ramírez-Valverde, 2021). Entonces, ¿las vacunas no ayudaron a reducir el contagio? Bueno, déjame te digo que para establecer estrategias de vacunación en grupos etarios se necesitaron de las matemáticas para detectar grupos más vulnerables o con altas probabilidades de fallecimiento (Salinas-Aguirre et al., 2022).
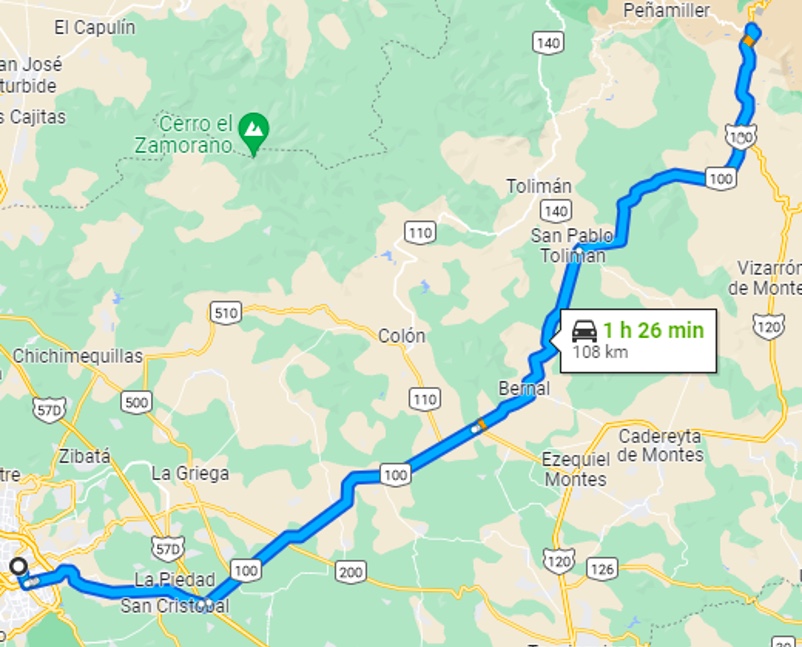
Imagina ahora que estás en el centro de la ciudad y debes regresar a tu casa. No sabes el estado del tráfico y te preguntas ¿cuál es la mejor ruta para llegar a mi domicilio? Lo primero que haces es sacar tu celular, abrir Google Maps o Waze y ver el estado actual del tráfico, así como la ruta más rápida. ¿Te has preguntado cómo funciona esto? Si te dijera que detrás de todo eso hay pensamiento matemático, ¿me lo creerías? La respuesta es sí, detrás de esas aplicaciones hay un método que resuelve el problema con el mejor resultado posible. Esta subcategoría del pensamiento matemático se llama estrategias heurísticas (EH). Definimos EH como el conjunto de estrategias de búsqueda para resolver un problema a partir de medios matemáticos concretos.
Podemos seguir listando ejemplos en los que el pensamiento matemático influye en nuestras decisiones o nos ayuda a entender lo que pasa a nuestro alrededor. El PM no son letras, números, raíces, factorizaciones, definiciones y teoremas. Es un recurso con el cual podemos describir y entender nuestro entorno. Atangana y Gómez-Aguilar (2018) en uno de sus artículos nos decían que las matemáticas deben obedecer las leyes de la naturaleza, y no es la naturaleza la que debe ajustarse a las reglas matemáticas.
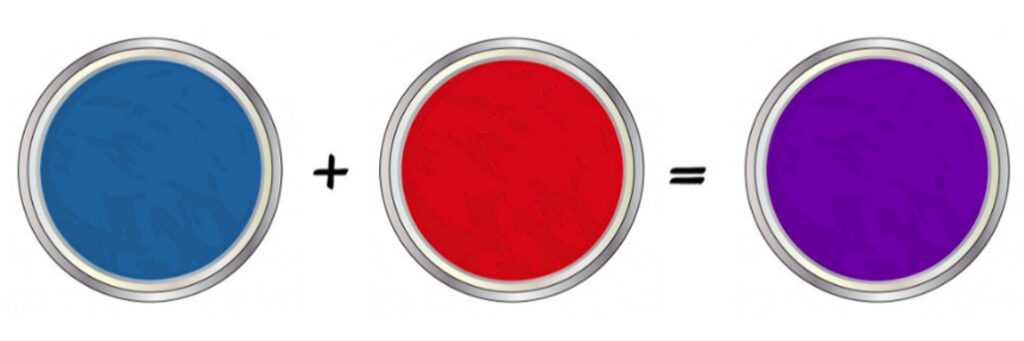
Pero, ¿realmente el pensamiento matemático que hemos aprendido a lo largo de nuestra educación escolar obedece las leyes de la naturaleza? Imagina que tienes dos vasos con pintura de color rojo y azul. Lo primero que haces es mezclar un poco de pintura roja con azul, y a la pintura combinada le vuelves a agregar azul. El resultado sería un color morado. ¿Pero qué pasaría si primero mezclas dos tantos de color azul y agregas el color rojo? ¿Obtienes el mismo resultado? La respuesta es no, el color que obtendrías es púrpura. Este ejemplo, aunque sea simple, es una muestra de que la asociatividad no aplica en la naturaleza. Entonces, ¿no podemos entender el mundo a través del PM?
Dentro de las matemáticas, tenemos una rama que se llama cálculo fraccionario. Este tipo de matemáticas nos permite describir fenómenos de nuestro entorno de una manera más precisa. Esta poderosa herramienta ha sido utilizada en campos de la ciencia, tecnología e ingeniería, en los que existen fenómenos complejos de entender. Por ejemplo, conocer la composición química del Sol, o los neutrinos solares en cosmología.
Entonces, ¿el pensamiento matemático con un enfoque fraccionario nos puede ayudar a entender el mundo? La respuesta es sí. La idea fundamental del cálculo fraccionario es el efecto de memoria. Esta propiedad particular nos permite entender y conocer qué ha pasado a lo largo del tiempo.
Una práctica que suelo poner a mis estudiantes de la materia de dinámica de sistemas físicos es la construcción de un circuito electrónico resistivo-capacitivo (RC). El objetivo es construir un modelo matemático y utilizarlo para representar lo que sucede en uno de los componentes. Específicamente el capacitor, el elemento de color azul que parece un barril (ver Figura 5).

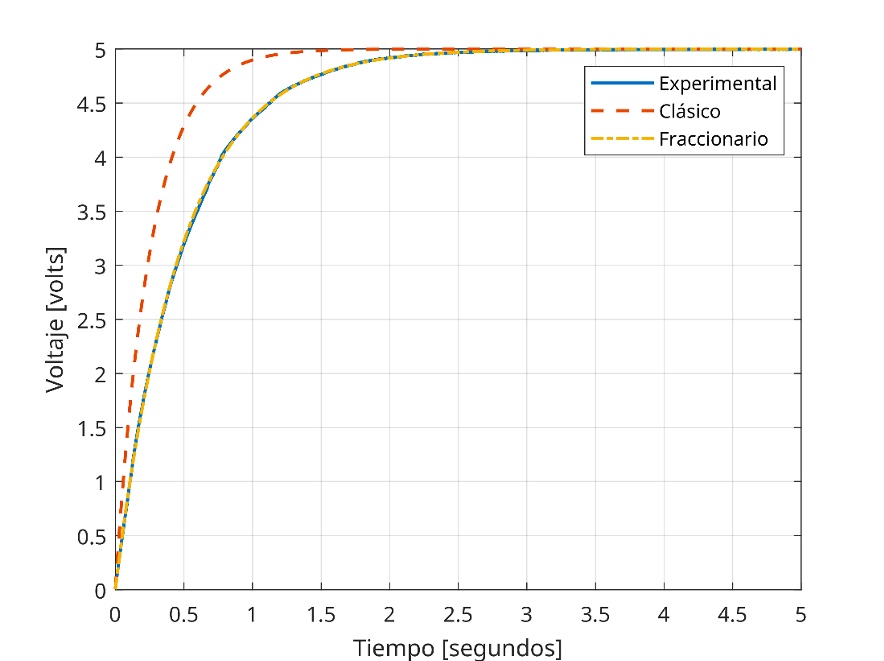
Cuando los estudiantes grafican los resultados que obtuvieron en la práctica, observan que el modelo que utilizaron no representa este fenómeno sencillo. ¿qué estrategias utilizamos para resolver este problema? Utilizamos PM con enfoque fraccionario. Es decir, construimos un modelo matemático fraccionario y lo utilizamos para describir lo que sucede en el capacitor. Esto lo podemos ver claramente en la Figura 6.
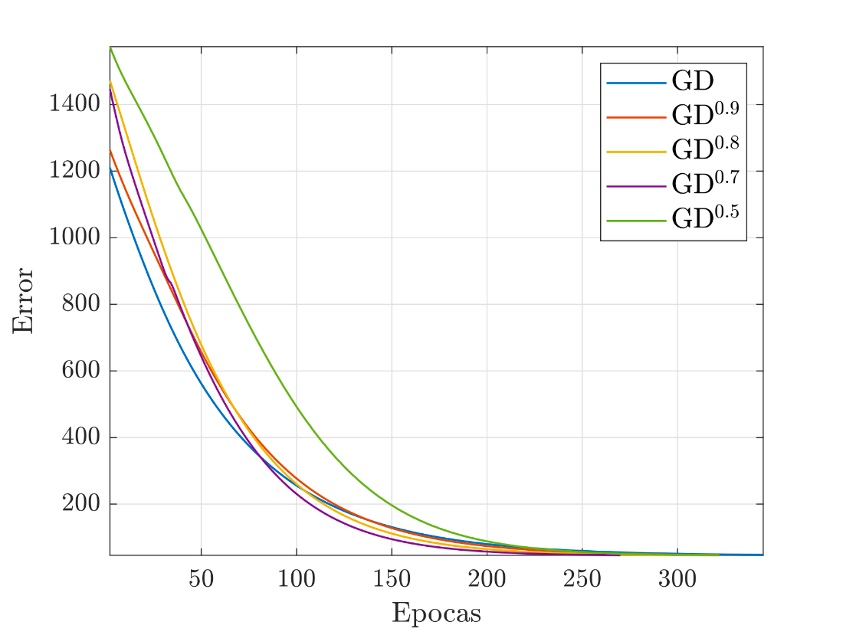
¿Es posible obtener heurísticas con enfoque fraccionario?, ¿qué ventajas tenemos con ello? Observamos que el tiempo de búsqueda se reduce y, por consiguiente, encontramos la solución a un problema en el menor tiempo posible. Esto se observa en la Figura 7.
El pensamiento matemático con enfoque fraccionario (PMEF) es tan antiguo como aquel que adquirimos desde la educación básica (Ozores, 2014). Sin embargo, es en los últimos años que se le ha dado especial atención por ser un enfoque poderoso.
El avance tecnológico y la evolución del conocimiento han permitido realizar cálculos que hace muchos años eran difíciles de hacer. El acceso a la información, la internet, así como las redes sociales, también han sido fundamentales en la difusión y divulgación de este pensamiento, pues basta con ingresar al buscador, teclear “aplicaciones de cálculo fraccionario” y encontrar algo de nuestro interés dentro de los 109,000 resultados que nos arroja el buscador.
¿Cuáles son los retos a los que nos enfrentamos al tratar de obtener un pensamiento matemático con enfoque fraccionario?
- Tratar de establecer conexiones con otras posibles áreas, por ejemplo: probabilidad, política, tecnología, cultura, economía, arte o el mundo social.
- Buscar estrategias para que conceptos tan abstractos como memoria, soluciones numéricas, integrales o derivadas de orden no entero sean cercanos a la experiencia de los estudiantes que deciden emprender el camino del PMEF.
- Impactar en otras áreas del pensamiento matemático. Por ejemplo:
- Elementos geométricos.
- Pensamiento algebraico.
Si estás interesado en conocer más de PM con enfoque fraccionario, puedes visitarnos en el siguiente enlace: https://fractionalcdiffusion.wordpress.com
Referencias
- Acuña-Zegarra, M. A., Santana-Cibrian, M., & Velasco-Hernandez, J. X. (2020). Modeling behavioral change and COVID-19 containment in Mexico: A trade-off between lockdown and compliance. Mathematical biosciences, 325, 108370.
- Atangana, A., & Gómez-Aguilar, J. F. (2018). Decolonisation of fractional calculus rules: breaking commutativity and associativity to capture more natural phenomena. The European Physical Journal Plus, 133, 1-22.
- Beleño, A. J. (2022). Competencias matemáticas para el desarrollo de habilidades cognitivas en estudiantes universitarios. Revista Latinoamericana de Difusión Científica, 4(7), 141-167.
- Aerodynamic drag in cycling team time trials. Journal of Wind Engineering and Industrial Aerodynamics, 182, 128-145.
- Repensar la evaluación para la mejora educativa. Resultados de México en PISA 2018; México: autor.
- De León, U. A. P., Pérez, Á. G., & Avila-Vales, E. (2020). An SEIARD epidemic model for COVID-19 in Mexico: mathematical analysis and state-level forecast. Chaos, Solitons & Fractals, 140, 110165.
- Domínguez-Morales, S., Pérez-Hernández, M., & Pérez-Sánchez, E. (2022). Ambientes de aprendizaje para favorecer competencias matemáticas en educación básica. Revista RedCA, 5(13), 144-162.
- Escalante, R., & Pacheco, F. (2005). Un modelo matemático para la bola de fútbol. Revista de Matemática: Teoría y Aplicaciones, 12(1-2), 97-109.
- Guzmán, F. (28 de noviembre de 2022). La evolución del balón en los mundiales. UNAM Global. https://unamglobal.unam.mx/global_revista/la-evolucion-del-balon-en-los-mundiales/
- Herrera-Aguilar, J. L., Contreras García, A. V., & Álvarez Herrera, C. (2019). ¿Dónde está la Física y las Matemáticas en los Deportes Olímpicos?. FINGUACH. Revista De Investigación Científica De La Facultad De Ingeniería De La Universidad Autónoma De Chihuahua, 3(8), 6,7. Recuperado a partir de https://vocero.uach.mx/index.php/finguach/article/view/267
- Lopes, J. E., Jacobs, D. M., Travieso, D., y Araújo, D. (2014). Predicting the lateral direction of deceptive and non-deceptive penalty kicks in football from the kinematics of the kicker. Human Movement Science, 36, 199-216.
- Macías-González, G. G., Caldera-Montes, J. F., y Salán-Ballesteros, M. N. (2019). Orientación vocacional en la infancia y aspiraciones de carrera por género. Convergencia, 26(80).
- Ozores, A. L. (2014). Cálculo Fraccionario y dinámica newtoniana. Pensamiento Matemático, 4(1), 77-105.
- Ramírez-Valverde, G., y Ramírez-Valverde, B. (2021). Modelo estadístico para defunciones y casos positivos de COVID-19 en México. EconoQuantum, 18(1), 1-20.
- Salinas-Aguirre, J. E., Sánchez-García, C., Rodríguez-Sanchez, R., Rodríguez-Muñoz, L., Díaz-Castaño, A., y Bernal-Gómez, R. (2022). Clinical characteristics and comorbidities associated with mortality in patients with COVID-19 in Coahuila (Mexico). Revista Clínica Española (English Edition), 222(5), 288-292.
- . Wikimedia Commons. Recuperado 17:13, abril 25, 2023 de https://commons.wikimedia.org/w/index.php?title=File:FWC_2018_-_Group_D_-_ARG_v_ISL_-_Photo_152.jpg&oldid=754014973.
- Yeadon, M. R., y King, M. A. (2017). Computer simulation modelling in sport. In Biomechanical evaluation of movement in sport and exercise (pp. 221-254). Routledge.
El doctor Jesús Emmanuel Solís Pérez es profesor en la Escuela Nacional de Estudios Superiores Unidad Juriquilla, de la Universidad Nacional Autónoma de México
AQUI PUEDES LEER TODAS LAS ENTREGAS DE “DESDE LA UNAM”, LA COLUMNA DE LA UNAM, CAMPUS JURIQUILLA, PARA LALUPA.MX
https://lalupa.mx/category/aula-magna/desde-la-unam/