Los desastres naturales han ido en aumento en las últimas décadas. Mediciones sobre evidencia global y su impacto en sistemas económicos se pueden encontrar en The shocks of natural disasters on NPLs [Chen et al., 2023]; es por ello cada vez más urgente contar con predicciones confiables para alertar a la sociedad antes de que afecten las áreas en riesgo. Para ese fin, la modelación matemática ofrece una amplia gama de beneficios y ayuda a la humanidad en diversas formas.
La modelación matemática permite abordar problemas complicados en diversas áreas, como la física, la biología, la ingeniería y la economía, entre otras. Al representar fenómenos del mundo real mediante ecuaciones y relaciones matemáticas, la comunidad científica puede analizar y predecir el comportamiento de una gran variedad de fenómenos, como los que ocurren en sistemas naturales, sociales y económicos. En particular, la dinámica de fluidos geofísicos se puede estudiar con base en leyes físicas que se escriben por lo general en forma de ecuaciones diferenciales parciales (EDPs); por ejemplo, las leyes físicas de conservación de masa, balance de momento y conservación de energía, algunas de ellas bastante conocidas, como las llamadas ecuaciones de Navier-Stokes. En Mathematical and Computational Models of Flows and Waves in Geophysics [Hernández-Dueñas and Moreles, 2022], el lector interesado puede encontrar una serie de aplicaciones usando modelación matemática para fenómenos en la atmósfera, el océano, superficies volcánicas y en el subsuelo.
En meteorología, la modelación matemática ayuda a predecir el clima y los desastres naturales. Las predicciones meteorológicas son valiosas para la gestión de recursos naturales, como el agua y la energía. Con el cambio climático en curso, las predicciones meteorológicas son indispensables para comprender y adaptarse a los patrones climáticos, que están en constante transformación. Con ello, podemos tomar medidas para enfrentar eventos climáticos más extremos y ayudar en la planificación de infraestructuras y políticas de adaptación.
En A Tropical Stochastic Skeleton Model for the MJO, El Niño, and Dynamic Walker Circulation [Thual et al., 2018], se puede encontrar un ejemplo del uso de modelos matemáticos para el análisis de fenómenos atmosféricos que afectan al clima global. Las predicciones meteorológicas son fundamentales para la seguridad, la planificación y pueden ser muy útiles en la toma de decisiones. Su disponibilidad y precisión son centrales para proteger vidas y bienes, mejorar la resiliencia frente a eventos climáticos extremos y avanzar en la investigación y comprensión del clima y la atmósfera. Véase por ejemplo The quiet revolution of numerical weather prediction [Bauer et al., 2015] para una revisión histórica de la revolución de la predicción del tiempo con herramientas numéricas.
Las predicciones meteorológicas son también esenciales para la planificación en sectores como agricultura, transporte, construcción y turismo. Por ejemplo, los agricultores pueden optimizar sus prácticas de siembra y cosecha en función del pronóstico del clima [Mase and Prokopy, 2014], mientras que las autoridades de transporte pueden tomar decisiones sobre rutas y cancelaciones debido a las condiciones climáticas adversas.
Por otro lado, la modelación oceánica es una herramienta poderosa que ayuda a la humanidad de diversas maneras. Nos permite estudiar y predecir el comportamiento de los océanos y sus interacciones con la atmósfera y la Tierra. La modelación oceánica es esencial para la predicción de eventos climáticos como huracanes, ciclones y tsunamis. Estos pronósticos permiten alertar a las comunidades y tomar medidas preventivas para proteger vidas y propiedades. Los modelos oceánicos ayudan a comprender cómo los océanos interactúan con la atmósfera y cómo estas interacciones influyen en el clima.
Estos modelos son esenciales para evaluar el aumento del nivel del mar, la acidificación oceánica y otros efectos en los ecosistemas marinos y costeros. La modelación oceánica es útil para predecir la distribución y migración de especies marinas, lo que ayuda a mejorar la pesca y la acuicultura de manera sostenible. Los modelos también se pueden utilizar para estudiar la dinámica de los ecosistemas marinos y su respuesta a la variabilidad ambiental. Los modelos oceánicos son fundamentales para la investigación científica y el estudio de procesos oceánicos complejos, como pueden ser las corrientes marinas. Entre otras aplicaciones, se puede analizar el papel que juega la interacción de distintas ondas en la dispersión horizontal oceánica, que en submesoescalas gobierna la propagación de contaminantes, plancton y colonia de peces. Véase Hernández-Dueñas et al., 2021, para un estudio numérico sobre este fenómeno.
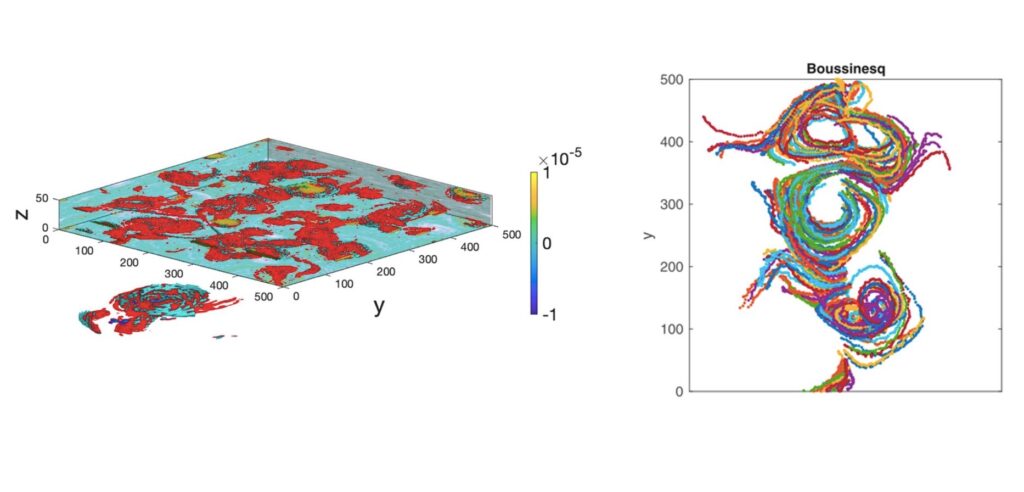
En la figura 1 se puede identificar la formación de vórtices en los flujos oceánicos (panel izquierdo) y cómo esto afecta la propagación horizontal de trazadores pasivos.
Referencias
- [Bauer et al., 2015] Bauer, P., Thorpe, A., and Brunet, G. (2015). The quiet revolution of numerical weather prediction. Nature, 525(7567):47–55.
- [Chen et al., 2023] Chen, X., Zhao, X., and Chang, C.-P. (2023). The shocks of natural disasters on NPLs: Global evidence. Economic Systems, 47(1):101050.
- [Hernández-Dueñas et al., 2021] Hernández-Dueñas, G., Lelong, M.-P., and Smith, L. M. (2021). Impact of wave–vortical interactions on oceanic submesoscale lateral dispersion. Journal of Physical Oceanography, 51(11):3495–3511.
- [Hernández-Dueñas and Moreles, 2022] Hernández-Dueñas, G. and Moreles, M. A. (2022). Mathematical and Computational Models of Flows and Waves in Geophysics. Springer Nature.
- [Mase and Prokopy, 2014] Mase, A. S. and Prokopy, L. S. (2014). Unrealized potential: A review of perceptions and use of weather and climate information in agricultural decision making. Weather, Climate, and Society, 6(1):47–61.
- [Thual et al., 2018] Thual, S., Majda, A. J., and Chen, N. (2018). A Tropical Stochastic Skeleton Model for the MJO, El Niño, and Dynamic Walker Circulation: A simplified GCM. Journal of Climate, 31(22):9261–9282.
El doctor Gerardo Hernández Dueñas es investigador en el Instituto de Matemáticas de la UNAM Juriquilla
Email: hernandez@im.unam.mx
AQUI PUEDES LEER TODAS LAS ENTREGAS DE “DESDE LA UNAM”, LA COLUMNA DE LA UNAM, CAMPUS JURIQUILLA, PARA LALUPA.MX
https://lalupa.mx/category/aula-magna/desde-la-unam/