Iniciemos nuestro paseo geométrico hablando de curvas.
Curvas
- La trayectoria que sigue un planeta en nuestro sistema solar, la cual, como sabemos desde Kepler, es una elipse.
- La trayectoria de una avioneta desde que despega hasta que aterriza.
- Una carretera que cruza los campos y cerros, digamos de Querétaro a San Miguel de Allende.
- La forma del cable de luz que cuelga entre dos postes. Tal curva se conoce como catenaria.
Ahora vamos a considerar dos clases de curvas especiales y relevantes en la navegación: curvas loxodromas y hélice.
Curvas loxodromas
Por ejemplo, un barco que navega en el mar y que mantiene un rumbo fijo describe una trayectoria, la cual es una curva loxodroma. Es sencillo mantener la ruta siguiendo tal curva, ya que basta seguir una dirección fija con ayuda de una brújula. Si modelamos la superficie del mar como parte de una esfera, resulta que los meridianos y los paralelos son curvas loxodromas, ya que en el primer caso es una curva donde la brújula nos marca siempre al norte o al sur. En el segundo caso nos marca siempre al este o al oeste.
Esta forma de navegar es más fácil de realizar que si intentamos viajar por la trayectoria de longitud más corta entre dos lugares determinados, es decir, por una geodésica. Así que las curvas loxodromas forman un ángulo constante con respecto a la dirección norte.
Curvas hélice
Ahora podemos pensar en curvas que están en nuestro espacio y que con respecto a la dirección vertical forman un ángulo constante. Tales curvas son similares a las curvas loxodromas y se conocen como curvas hélice[1]. Están caracterizadas por el hecho de que su torsión dividida entre su curvatura es una constante. La curvatura en un punto de una curva mide qué tanto se parece a una línea recta alrededor de ese punto. Similarmente, su torsión mide qué tan plana es la curva cerca de un punto.

Continuemos nuestro paseo con superficies.
Superficies
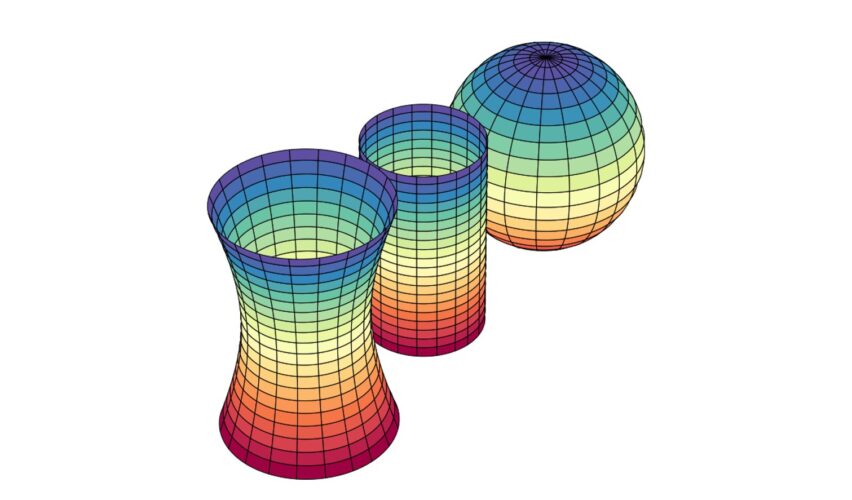
- La forma de la córnea del ojo humano se puede modelar como una superficie de revolución, la cual tiene un eje de simetría. Cuando esa simetría se perturba, también la curvatura del ojo cambia y se puede presentar la miopía en la visión.
- La forma de la superficie del terreno en el campo que consta de cerros y praderas.
- La superficie de nuestro cuerpo.
- La superficie de una antena parabólica, la cual es un paraboloide de revolución y gracias a sus propiedades geométricas podemos recibir señales de telecomunicaciones.
- La delgada película de jabón que se forma cuando sumergimos un alambre cerrado en una solución jabonosa. Estas superficies son llamadas mínimas.
Superficies hélice
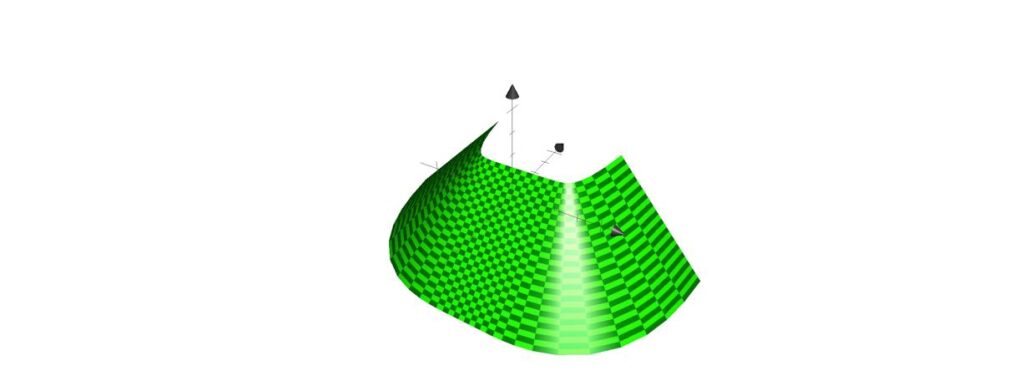
Otra clase de superficies son las superficies de ángulo constante o hélice. Se empezaron a estudiar en 2007. Son superficies en nuestro espacio en las que, al igual que las curvas hélice, el ángulo que forma con la dirección vertical es constante (vea la Figura 2).
Un plano inclinado es el ejemplo más sencillo. También un cono de revolución cuyo eje de revolución es vertical.
Se ha demostrado que estas superficies hélice son regladas. Se construyen con el siguiente algoritmo[2]:
- Se empieza dibujando una curva regular en el piso. Se elige un ángulo entre 0 y 90 grados.
- Se pega una recta en cada punto de la curva. Tal recta debe ser ortogonal a la curva y formar el ángulo elegido con respecto a la dirección vertical.
Acerca de la curvatura gaussiana y media
Aquí cabe mencionar que una superficie en nuestro espacio tiene dos tipos de curvatura: gaussiana y media. La primera es una propiedad geométrica intrínseca y la segunda extrínseca.
La curvatura de una superficie en un punto se puede determinar con ayuda de la curvatura de las curvas dentro de la superficie y que pasan por ese punto. Resulta que dentro de todas esas curvas hay una que tiene la máxima curvatura, y otra curva perpendicular a la primera y que tiene curvatura mínima en el punto en cuestión. Estas curvaturas máxima y mínima se conocen como curvaturas principales de la superficie en ese punto[3]. Por ejemplo, en una superficie de revolución, las curvaturas principales se alcanzan en los paralelos y meridianos. En una superficie hélice, una de las curvaturas principales vale cero y se alcanza en las rectas que generan a la superficie.
La curvatura gaussiana es el producto de las curvaturas principales. La curvatura media es el promedio de las curvaturas principales. En particular, la curvatura gaussiana de una superficie hélice es constante cero. El plano y un cono de revolución son ejemplos de superficies hélice y son de curvatura gaussiana cero. La curvatura gaussiana de la cornea de un ojo es positiva.
Las superficies de curvatura media constante cero se llaman superficies mínimas: como las del alambre en la solución de jabón. Una esfera tiene ambas curvaturas, gaussiana y media, constantes. Las superficies de revolución de curvatura media constante no cero están clasificadas y se conocen como superficies de Delaunay.
Conclusión
A pesar de su similitud con las curvas hélice, sólo en años recientes se han investigado tales superficies.
Será interesante descubrir que aplicaciones pueden tener. Por ejemplo, se sabe que aparecen en la interface de dos cristales líquidos[4].
Referencias
[1] A. Gray ; E. Abbena; S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, Stud. Adv. Math. Chapman & Hall/CRC, Boca Raton, FL, 2006.
[2] A. J. Di Scala and G. Ruiz-Hernández, Helix submanifolds in euclidean spaces, Monatsh. Math. 157 (2009), 205–215.
[3] A. Gray ; E. Abbena; S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, Stud. Adv. Math. Chapman & Hall/CRC, Boca Raton, FL, 2006.
[4] P. Cermelli and A. J. Di Scala, Constant-angle surfaces in liquid crystals, Philosophical Magazine, 87 (2007), 1871–1888.
El doctor Gabriel Ruiz Hernández es investigador en el Instituto de Matemáticas de la UNAM Campus Juriquilla.
AQUI PUEDES LEER TODAS LAS ENTREGAS DE “DESDE LA UNAM”, LA COLUMNA DE LA UNAM, CAMPUS JURIQUILLA, PARA LALUPA.MX
https://lalupa.mx/category/aula-magna/desde-la-unam/