El estudio de los fenómenos naturales siempre nos lleva (nos guste o no) al análisis de problemas matemáticos. Es interesante el hecho de cómo varios problemas que surgen en biología, química y, sobre todo, en física pueden traducirse al lenguaje matemático. La idea de una ecuación diferencial es recuperar una (o varias) funciones cuyas derivadas satisfagan la ecuación en cuestión. A diferencia de una ecuación algebraica de segundo orden, como las que uno estudia en la secundaria o preparatoria y que se resuelven con la chicharronera[1], en este caso debemos encontrar una función que resuelva dicha ecuación.
Quizás el lector se pregunte ¿por qué es importante resolver este tipo de ecuaciones? Por ejemplo, la ecuación de crecimiento exponencial modela procesos como el crecimiento poblacional. Esta sencilla ecuación describe el comportamiento básico de muchos sistemas biológicos y económicos. En física avanzada, encontramos ejemplos como la ecuación del oscilador de Lorentz, que nos ayuda a entender la interacción de la luz con materiales ópticos. Por otro lado, en el estudio de ondas electromagnéticas, la ecuación de propagación de ondas permite analizar la transmisión de luz en medios como las fibras ópticas. Por último, en el ámbito de la física cuántica, la ecuación de Schrödinger independiente del tiempo describe el comportamiento de partículas, por ejemplo, los electrones. Y así podríamos seguir con más ejemplos.
Además, están las razones puramente matemáticas por la que estos problemas son importantes. Cualquier problema que conlleve el reto de probar la existencia de soluciones es interesante, por los métodos y herramientas que uno tiene que desarrollar para resolverlo. El estudio de las ecuaciones diferenciales surgió a la par que el desarrollo del cálculo diferencial e integral (aquí el lector tome su bando, si es team Newton o Leibniz). Estas herramientas surgieron en el siglo XVII, y fueron desarrolladas por grandes matemáticos como Bernoulli (siglo XVII), Laplace y Lagrange (siglo XVIII), Cauchy (siglo XIX), y Peano, Picard y Hilbert (siglos XIX y XX). En el caso de un matemático aplicado (como lo es el segundo autor), hay un interés primordial: ¿Cómo construyo las soluciones? Por poner un ejemplo, si una ecuación surge de analizar un proceso en biología (como pueden ser aquellas que describan el comportamiento de una pandemia, como la que acabamos de vivir), un epidemiólogo no va a estar interesado sólo en saber que la solución existe, sino en cómo calcularla de forma práctica. Vamos a poner como ejemplo la siguiente ecuación diferencial, la cual ha sido el objeto de estudio de ambos autores:
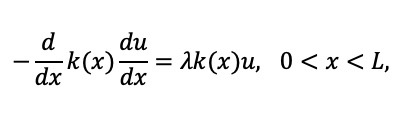
Esta ecuación recibe el nombre de ecuación de Sturm-Liouville en forma de impedancia, y es un caso particular de un tipo de ecuaciones estudiadas a finales del siglo XIX por Jacques Sturm y Joseph Liouville. El problema consiste en encontrar los números λ (eigenvalores) para los cuales existe una solución (eigenfunción) que satisface las condiciones de Dirichlet u(0) = u(L) = 0.
Para un físico (como lo es la primera autora), este tipo de ecuaciones son importantes, pues aparecen en el estudio de fenómenos donde se analiza la propagación de ondas, vibraciones y resonancias. Esta ecuación se utiliza para modelar sistemas físicos donde existe un cambio espacial en las propiedades del medio, como ocurre en materiales heterogéneos o medios con variaciones de densidad. Hablaremos de dos ejemplos. El primero es el análisis de modos de vibración de una cuerda o membrana cuando se somete a ciertas condiciones de frontera (como fijar los extremos, que corresponderían a las condiciones de Dirichlet). Los eigenvalores están relacionados con las frecuencias naturales de vibración del sistema. Estos valores indican a qué frecuencias específicas el sistema puede resonar, produciendo una oscilación estable. Por su parte, en óptica, una aplicación de este tipo de ecuaciones es el diseño de guías de onda y fibras ópticas. Las eigenfunciones describen los modos de propagación de la luz a través de una guía de onda, donde el índice de refracción del material cambia con la posición. Los eigenvalores corresponden a los modos de resonancia, es decir, los estados en los que la luz se propaga sin pérdidas significativas, permitiendo una transmisión eficiente de señales. En resumen, estas soluciones describen cómo se comporta un sistema bajo ciertas condiciones específicas, y los eigenvalores nos dan información sobre las frecuencias o las energías asociadas a estos estados. Por esta razón, encontrar estos valores y funciones es importante para entender y predecir el comportamiento de sistemas físicos en diversos campos.
Para atacar esta ecuación, decidimos utilizar un método desarrollado en Kravchenko y Porter, 2010[2]: el llamado método de series de potencias del parámetro espectral (SPPS por sus siglas en inglés). Este fue desarrollado por el Dr. Vladislav Kravchenko y el Dr. Michael Porter, ambos investigadores del Cinvestav Querétaro. El método se basa en representar las soluciones de la ecuación como series de potencias en el parámetro λ. Resulta que estas representaciones son bastante sencillas de calcular en la computadora, empleando métodos de integración que uno aprende en los cursos de análisis numérico e implementando el algoritmo en numpy, de manera que uno puede obtener con bastante precisión y rapidez las eigenfunciones. Por ejemplo, en la siguiente figura vemos algunas eigenfunciones para cuando k (x) = 1 + sin(x).
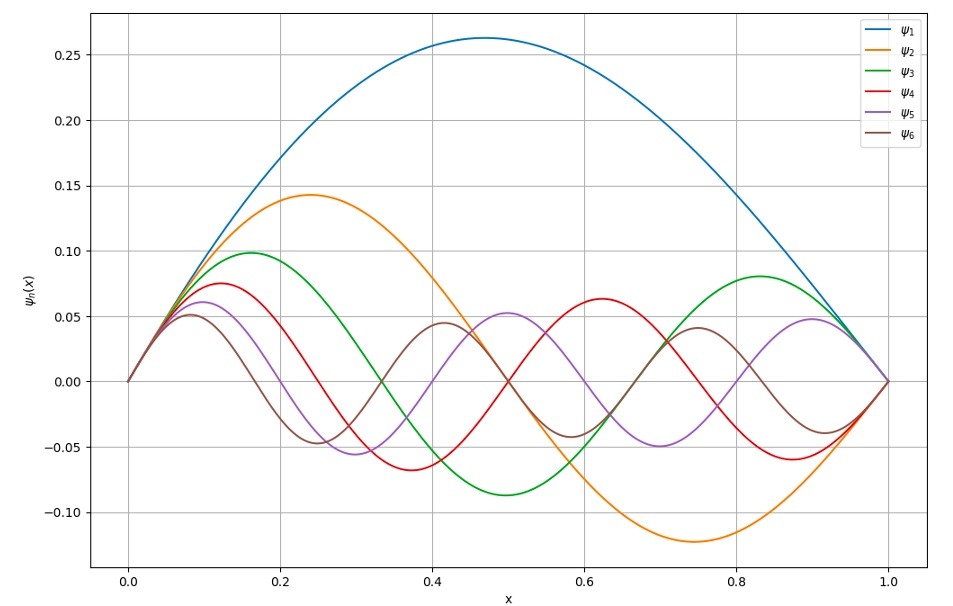
En física, las eigenfunciones obtenidas con el método SPPS tienen una interpretación como modos de vibración del sistema. En el caso de la ecuación de Sturm-Liouville con impedancia variable, estas soluciones representan los patrones de onda estacionaria que se establecen en un medio donde las propiedades (como la densidad o la rigidez) varían con la posición. Este tipo de análisis es común en problemas de vibración mecánica, acústica y óptica.
En acústica, estas eigenfunciones pueden interpretarse como los modos de vibración de una cuerda o membrana cuyo material cambia a lo largo de su longitud, generando patrones de oscilación complejos. Los valores altos y bajos de las eigenfunciones indican las regiones donde la vibración es máxima (antinodos) y mínima (nodos), respectivamente. En óptica, si consideramos estas eigenfunciones en el contexto de una guía de onda con un índice de refracción que varía, los patrones de las eigenfunciones describen los modos de propagación de la luz dentro de la guía. Cada eigenfunción corresponde a un modo específico de propagación, donde la luz se distribuye según el perfil de la eigenfunción, lo que determina cómo se concentra y se disipa la energía en la guía. En resumen, las eigenfunciones proporcionan una representación visual y matemática de los modos naturales del sistema, permitiendo predecir el comportamiento de la vibración o la propagación de ondas en medios con propiedades variables.
El análisis de las ecuaciones de Sturm-Liouville mediante el método SPPS demuestra ser una herramienta robusta para la comprensión de fenómenos físicos complejos. La combinación de técnicas analíticas y numéricas permite no sólo identificar los eigenvalores y eigenfunciones con alta precisión, sino también entender mejor las propiedades fundamentales de los sistemas físicos modelados. La moraleja es que existen métodos numéricos modernos que nos permiten obtener resultados muy eficientes, y que son bastante sencillos de implementar. El uso de métodos numéricos avanzados y su implementación accesible en Python subrayan la importancia de integrar estas técnicas en la enseñanza de ecuaciones diferenciales, ofreciendo a los estudiantes una perspectiva moderna y aplicada. Este enfoque contribuye a una mejor formación científica y facilita el estudio de problemas de física-matemática actuales.
[1] En México, se llama coloquialmente chicharronera a la fórmula general para resolver la ecuación de segundo grado.
[2] Kravchenko, Vladislav V., and Robert Michael Porter. “Spectral parameter power series method for Sturm-Liouville problems.” Mathematical Methods in the Applied Sciences, 33 (2010), pp. 459-468.
Abigail Guadalupe Márquez Hernández actualmente es estudiante de la licenciatura en física en la División de Ciencias e Ingenierías de la Universidad de Guanajuato. El doctor Víctor Alfonso Vicente Benítez es posdoctorado en el Instituto de Matemáticas de la UNAM, Unidad Juriquilla.
AQUI PUEDES LEER TODAS LAS ENTREGAS DE “DESDE LA UNAM”, LA COLUMNA DE LA UNAM, CAMPUS JURIQUILLA, PARA LALUPA.MX
https://lalupa.mx/category/aula-magna/desde-la-unam/