Durante esta pandemia habrás escuchado con frecuencia la expresión: “crece exponencialmente”. En general, me parece, que todos comprendemos que esto se refiere a que algo crece mucho o crece muy rápido. Sin embargo, la mayoría de la gente no imagina lo “mucho” o “rápido” que una función exponencial crece realmente. El objetivo de este escrito es contribuir al entendimiento de este fenómeno.
No seré muy técnica. No es mi intención definir formalmente lo que es una función ni, particularmente, lo que es una función exponencial. Apelaré más a tu intuición proporcionándote algunos ejemplos más o menos concretos.
Para empezar, visualicemos algunas magnitudes. Cuando hablamos de números pequeños nos es fácil imaginar lo que estos representan. Por ejemplo, si te digo un número del orden de 10, como 5 u 8, te será sencillo pensar en los dedos de tu mano o visualizar los tentáculos de un pulpo. Ahora, si hablamos de un número del orden de 100, podrás pensar en algún conjunto que contenga entre 10 y 100 elementos (por ejemplo, el número de letras que contiene nuestro alfabeto o el número de palabras que hay en este párrafo).
Conforme aumentamos el orden (de 10, de 100, de 1000, de 10000…), nos costará más trabajo visualizar conjuntos que representen dichas magnitudes. Para darte una idea concreta, en la ilustración 1, se muestran: 100, 1000 y 10000 puntos respectivamente.

Como ya sabes, 100 es 10 veces 10 de la misma manera que 1000 es 10 veces 100. Lo anterior se expresa utilizando la llamada notación científica de la siguiente manera:
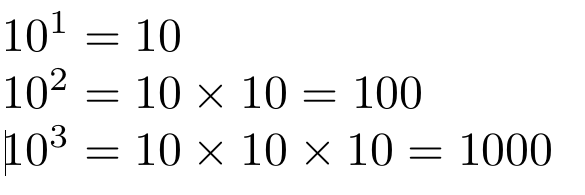
donde el número pequeño arriba del 10, que se llama exponente, es el que determina el número de veces que hemos de multiplicar al número 10 consigo mismo, dando como resultado, en nuestra notación decimal, un 1 seguido de tantos ceros como el exponente indique. Por ejemplo: 10 elevado al exponente 6, da como resultado un millón, 1000000.
Un millón es, quizás, un número que mucha gente aún pueda concebir (¿tú también pensaste en qué harías con esa cantidad de dinero?). Para ilustrar la magnitud de 106 con los puntos, como hicimos en la ilustración 1, necesitaríamos aproximadamente la superficie de un metro cuadrado. ¿Te imaginas qué superficie necesitaríamos para representar con puntos 109? ¡Cada vez es más difícil tener una idea acertada! Para ilustrar 109, es decir: un 1 seguido de nueve ceros, tendríamos que llenar de puntos, más o menos, una superficie equivalente a dos canchas de básquetbol. Sorprende saber que al orden de 109 pertenecen por ejemplo el número de segundos en un siglo o de seres humanos vivos al día de hoy.
Lo que estamos haciendo es analizar la función exponencial con base 10. Esto es una función que para el número 1 vale 10, para el 2 vale 100, y para un cierto numero “ vale 10x. Tal vez no te haya sorprendido que para el noveno paso (es decir, 109), esta función alcance un valor del orden del número de seres humanos vivos, pero piensa en los negocios (que yo llamaría más bien estafas) llamados “pirámides” con los que, de modo recurrente, pretenden tentarnos: si entran 10 personas y ponen mil pesos, pero además cada una invita a otras 10 personas con sus respectivos mil pesos cada una, y estas también invitan a otros 10 estafados, ¡el que inició la pirámide podrá tener el millón de pesos en el que pensabas hace rato!, pero la pirámide resulta insostenible pues en el noveno paso tendrían que estar involucrados no solo todos los habitantes de Querétaro sino del mundo entero.
Continuemos analizando el crecimiento de la función exponencial con base 10. ¿Qué pasa si duplicamos el exponente? Es decir, tenemos una idea de cuánto es 109 pero ¿cuánto será 1018? No es mucho el incremento, ¿o sí?
Resulta que del orden de 1018 es el número de átomos que hay en un grano de arena, como también el número de granos de arena en el planeta. ¡Sorprendente!, ¿no?

Imagina ahora cuál es el orden del número de átomos en el mundo. O vayamos más allá, ¿cuál será el orden del número de átomos en el universo?
No sé muy bien cómo es que los físicos estiman dichas magnitudes, pero es un consenso que el orden del número de átomos en el universo es 1080. No parece mucho, pero eso es, ¡el orden del número de átomos en el universo es 1080. Así de rápido es como crece una función exponencial.
El crecimiento de una epidemia como la que vivimos en estos momentos suele ser exponencial. Para controlar o reducir dicho crecimiento se debe disminuir el R0, número básico de reproducción, del cual probablemente hayas escuchado hablar (es el número promedio de nuevos casos que genera un solo infectado). La mitigación social es una de las medidas más efectivas para reducir ese R0.
Con cada vez con mas frecuencia, he escuchado a la gente decir que las medidas de mitigación social adoptadas o impuestas por la mayoría de los gobiernos con el fin de controlar la epidemia causada por el nuevo virus SARS-CoV-2, son peores que la misma epidemia. Pero no. Lo que sucede es que quizás no comprendemos realmente los alcances de esta nueva enfermedad.