Muchas veces en mi vida, al contarle a algún desconocido lo que hago, me he topado con la siguiente situación:
—Soy matemática, hago investigación —les digo.
—¡Wow! ¿Y como qué investigas? ¿Buscas números? —me dicen, dejando entrever una sonrisa algo burlona.
Es curioso, pero me parece que esas dos palabras, matemáticas e investigación, llevan en casi todas las cabezas, de forma directa, a los conceptos número y búsqueda. Cuando formulo mi respuesta las reacciones varían, llevándose ya sea un fiasco, porque la broma no fue tan acertada, o mostrando verdadera sorpresa. Porque, lo crean o no, sí, yo busco números. Entre otras muchas cosas, una que hago y que despierta en mí verdadera pasión es buscar números.
Hay muchos números famosos en matemáticas: pi, el número de Euler, la razón áurea y montones de constantes llamadas por los nombres de sus descubridores, la mayoría con una infinidad de cifras decimales. Pues bien, en combinatoria (el área de las matemáticas que se dedica al “arte de contar”) hay muchos números enteros (es decir, sin decimales) verdaderamente enigmáticos. Por ejemplo, imaginemos que ponemos los números del 1 al 9 escritos cada uno con color rojo o azul, al azar. Existen 512 maneras de hacer esto: dos posibles colores para el 1, dos posibles colores para el 2, etc., es decir, 29 = 512 posibles configuraciones. Resulta que, en todas ellas, hay siempre tres números del mismo color (los tres rojos o los tres azules), de tal forma que los dos más pequeños suman al tercero. Un ejemplo se puede ver en la Figura 1.1.
Claramente, si tenemos más de nueve números, esto seguirá funcionando (porque podemos concentrarnos en los nueve primeros). En cambio, esto no funciona si sólo usamos los números del 1 al 8. En la Figura 1.2 podemos ver una configuración que no tiene ni tres números rojos ni tres azules que cumplan lo deseado. Si usamos tres colores diferentes, entonces pasa algo similar: pongamos como pongamos los números del 1 al 24 de rojo, azul o verde (lo que da 324 = 282,429,536,481 posibles configuraciones), siempre podremos encontrar tres del mismo color en donde la suma de los dos menores es igual al tercero (Fig. 1.3).
Sin embargo, existe una configuración de cómo colorear los números del 1 al 23 en donde esto no es posible (Fig. 1.3). Esta situación se puede formular para el número de colores que deseemos usar: existe un número mágico (sk) tal que, si coloreamos los números del 1 a n con k colores, en donde n es un número mayor o igual a sk, siempre habrá tres del mismo color en donde los dos primeros sumen al tercero. En cambio, existe una configuración con sk-1 números y k colores en donde esto no es posible. Esta es una versión (algo más fuerte) del famoso Teorema de Schur[1].

La cuestión aquí es que esos números mágicos no son tan fáciles de encontrar. Es, en realidad, extremadamente difícil encontrarlos. Del Teorema de Schur se conocen los números para hasta cinco colores. El número de Schur para cinco colores (que es 161) se descubrió muy recientemente, en 2018, haciendo un uso muy sofisticado de la computadora[2]. Además, si contemplamos algunos colores más, son números que acaban siendo gigantescos. Por ejemplo, se conoce una configuración del 1 al 99,209 con 10 colores, en donde no hay tres del mismo color que cumplen lo requerido (ver Ramsey Theory on the Integers[3]). Es decir, el número s10 debe ser mayor a 99,209.
Pero esto no es nada. En esta rama de la combinatoria, llamada Teoría de Ramsey por el matemático pionero Frank P. Ramsey (1903–1930), existen números mágicos todavía más sorprendentes. El Teorema de van der Waerden[4], por ejemplo, muestra que existe un número mágico wk tal que si “coloreamos” los primeros wk números enteros con cierto número k de colores siempre existirán tres números formando una progresión aritmética de un mismo color. No voy a explicar qué es una progresión aritmética, porque en este momento ese no es el punto. Tampoco quiero hablar de lo bonito y sorprendente que es este teorema. Me quiero concentrar en cómo esos números mágicos, los números de van der Waerden, rápidamente pasan a ser, ya no se diga gigantescos, sino completamente desorbitantes e inalcanzables. Por ejemplo, el Teorema de van der Waerden, para cinco colores y progresiones aritméticas de cinco términos, se sabe que funciona si coloreamos los números del 1 al:
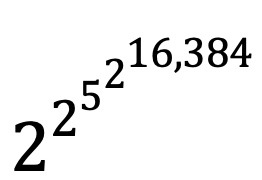
Para hacerse una muy vaga idea de qué tan grande es ese número, veamos que sólo la parte del exponente en donde aparece el 216,384 es un número mucho, pero mucho, más grande que el número de partículas que se estima tiene nuestro universo[5]. ¡Estamos pues hablando de una verdad matemática que considera un número entero que no podemos siquiera imaginar!
Los problemas que conciernen a estos números mágicos suelen ser extremadamente difíciles de resolver, lo cual no sólo trae en sí un atractivo reto para los matemáticos, sino que deriva en el desarrollo de la matemática de manera sustancial. Es así como surgió y creció el área, actualmente muy activa, de la Teoría de Ramsey, la cual, además, tiene un sinfín de aplicaciones en diversas otras áreas de las matemáticas, e incluso en otras ciencias[6]. El hablar con certeza de cosas que sólo se sabe a través del razonamiento matemático, pero que son imposibles de alcanzar físicamente, imposibles siquiera de imaginar porque no son comparables con nada físico, el saber que existen (en el mundo de las matemáticas), esos objetos tan intangibles son para muchos matemáticos, como yo, razones más que suficientes para estar enamorados de lo que hacemos.

Referencias
[1] Schur, Issai. Über die Kongruenz xm + ym = zm (modp), Jahresbericht der Deutschen Mathematikervereinigung, 25 (1917), 114–117.
[2] Marijn J.H. Heule, Schur Number Five, arXiv:1711.08076 (2017).
[3] Landman, Bruce, Robertson, Aaron. Ramsey Theory on the Integers, Stud. Math. Libr. 73, American Mathematical Society, Providence, RI, 2014, xx+384 pp.
[4] van der Waerden, Bartel, Beweis einer Baudetschen Vermutung, Nieuw. Arch. Wisk. 15 (1927), 212–216.
[5] Munafo, Robert, Notable Properties of Specific Numbers, http://mrob.com/pub/math/numbers-19.html
[6] Rosta, Vera, Ramsey Theory applications, Electron. J. Combin. 11 (2004), no. 1, Research Paper 89, 48 pp.
La doctora Adriana Hansberg es investigadora en el Instituto de Matemáticas de la Unidad Juriquilla de la UNAM
AQUI PUEDES LEER TODAS LAS ENTREGAS DE “DESDE LA UNAM”, LA COLUMNA DE LA UNAM, CAMPUS JURIQUILLA, PARA LALUPA.MX
https://lalupa.mx/category/aula-magna/desde-la-unam/