Autoría de Josué• 14 julio, 2024• 2:47 pm• Desde la UNAM • One Comment

Las matemáticas que salvan vidas: El cálculo fraccionario en la medicina – Jonathan Diego Pereyra y Jesús Emmanuel Solís

Las imágenes médicas son fundamentales en el diagnóstico y tratamiento de enfermedades. Estas técnicas, que incluyen radiografías, resonancias magnéticas, tomografías computarizadas y ultrasonidos, permiten a los profesionales de la salud visualizar órganos, tejidos y hasta los huesos del cuerpo. Según Smith-Bindman et al. (2008), facilitan la detección temprana de anomalías, la planificación de intervenciones quirúrgicas y el seguimiento de tratamientos.

De acuerdo con Cha (2014) y Gould et al. (2015), las imágenes médicas muestran una alta eficacia al momento de realizar un diagnóstico por profesionales de la salud, variando su precisión según el tipo de imagen que se utilice. Por ejemplo:

Tomografía computarizada (TC). Alta precisión en la detección de cáncer de pulmón, con un acierto del 90 %.
Resonancia magnética (MRI). Precisión del 95 % en diagnóstico de tumores cerebrales y en enfermedades musculoesqueléticas.
Mamografías. Entre 70 % y 90 % en la detección de cáncer de mama.
Ultrasonido. Altamente eficaz en obstetricia y ginecología, con un 95 % en la evaluación de la vesícula biliar, aunque su precisión puede variar según las condiciones del paciente.

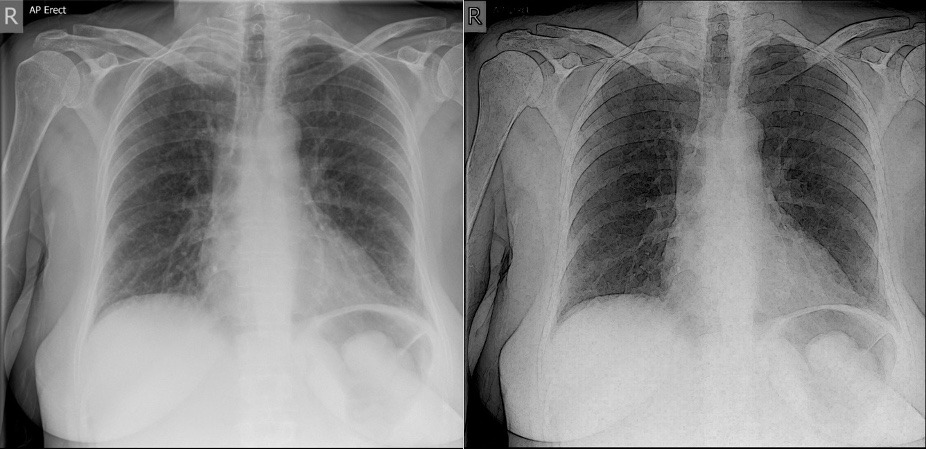
Imagina que estás en el consultorio médico esperando los resultados de una TC o una MRI. El doctor tiene una imagen que le ayudará a diagnosticarte, pero en lugar de ser una imagen nítida y clara, es borrosa, con falta de contraste o presenta ruido; esto se vuelve difícil de interpretar, ¿te ha pasado alguna vez? Este es un problema común en el mundo de las imágenes médicas.

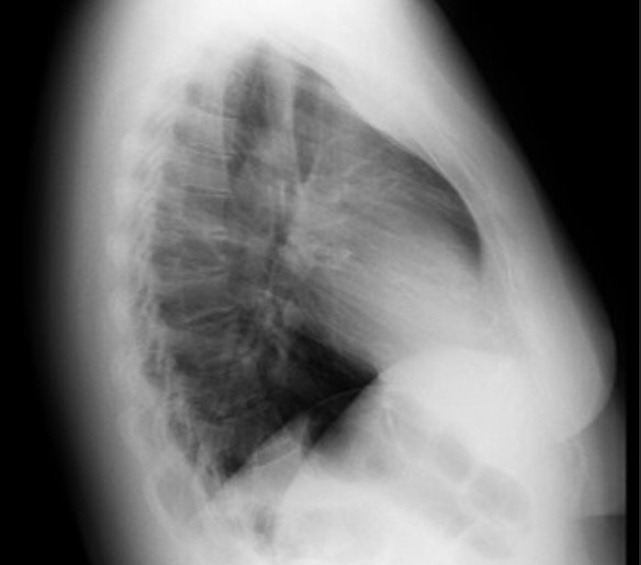
Figura 1. Imagen de resonancia magnética borrosa recuperada de https://carprimur.com.

Sin embargo, con los avances en tecnología de imágenes médicas se han ido mejorado. Hay una rama de las matemáticas en auge que promete revolucionar este campo: el cálculo fraccionario (CF). Aunque aún se encuentra en proceso de implementación en dispositivos de bajos recursos, el cálculo fraccionario ha demostrado ser una herramienta poderosa para mejorar la precisión y la calidad de las imágenes médicas.

Pensemos en una resonancia magnética del cerebro. Cuando los médicos utilizan esta técnica para ver dentro de nuestras cabezas, obtienen imágenes que no siempre son claras. Aquí es donde entra el CF. Al aplicar estos conceptos matemáticos avanzados, se puede mejorar la calidad de estas imágenes sin necesidad de realizar demasiados procesos de procesamiento.

En diversos trabajos, el CF ha demostrado ser una herramienta eficaz para reducir el ruido en las imágenes médicas, haciendo que los detalles pequeños sean más visibles. Esto es crucial cuando se trata de detectar tumores pequeños o anomalías sutiles que podrían pasarse por alto con técnicas de imagen tradicionales.

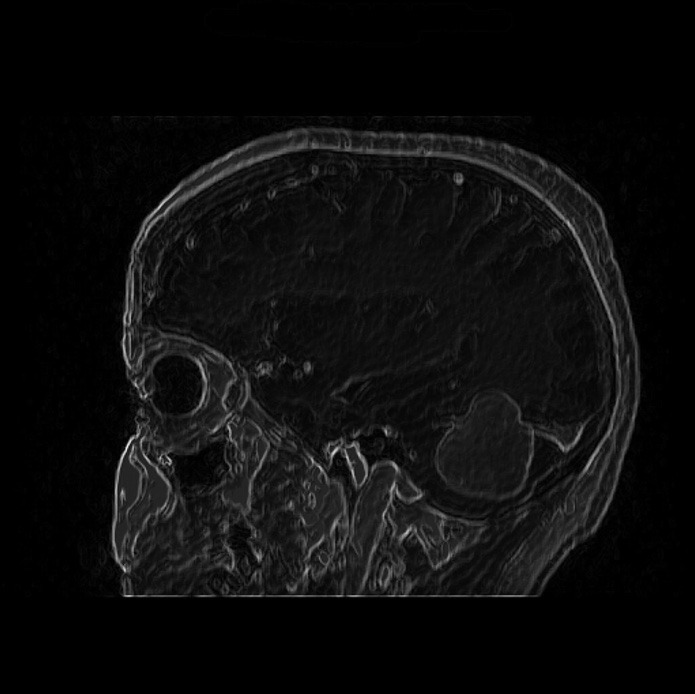
Figura 2. Imagen procesada con cálculo fraccionario.

Además, el CF permite reconstruir imágenes aumentando la calidad y perspectiva visual. Esto significa que los pacientes podrían pasar menos tiempo en las máquinas de escaneo y recibir menos radiación, algo importante para niños o personas que necesitan múltiples escaneos.

¿Pero qué es exactamente el cálculo fraccionario?

El cálculo fraccionario es una extensión del cálculo tradicional que nos permite trabajar con derivadas e integrales de orden no entero. En otras palabras, mientras que en el cálculo normal solemos hablar de la primera derivada, la segunda derivada, etcétera, el cálculo fraccionario nos permite considerar, por ejemplo, la derivada de orden 1/2 o 3/4.

Macías-Díaz (2022) menciona que este tipo de cálculo es útil en muchas áreas de la ciencia y la ingeniería, tales como la física, la química y la teoría de control, en las que a veces necesitamos describir fenómenos que no se ajustan bien a los modelos del cálculo tradicional.

¿Cómo podemos utilizar el cálculo fraccionario en la medicina?

Yin et al. (2020) desarrollaron un método que utiliza el CF para atenuar el ruido en las imágenes médicas. Es parecido a que si tuvieras un par de gafas mágicas que pueden filtrar toda la estática y dejar sólo los detalles importantes. Esto es importante cuando los médicos buscan pequeñas anomalías. También, Huang et al. (2019) han utilizado el CF para mejorar la restauración de imágenes médicas. Imagina que tienes una foto antigua y sin color, su método es como un restaurador digital que puede devolver la imagen a su gloria original, pero en este caso está trabajando con imágenes del interior de tu cuerpo.

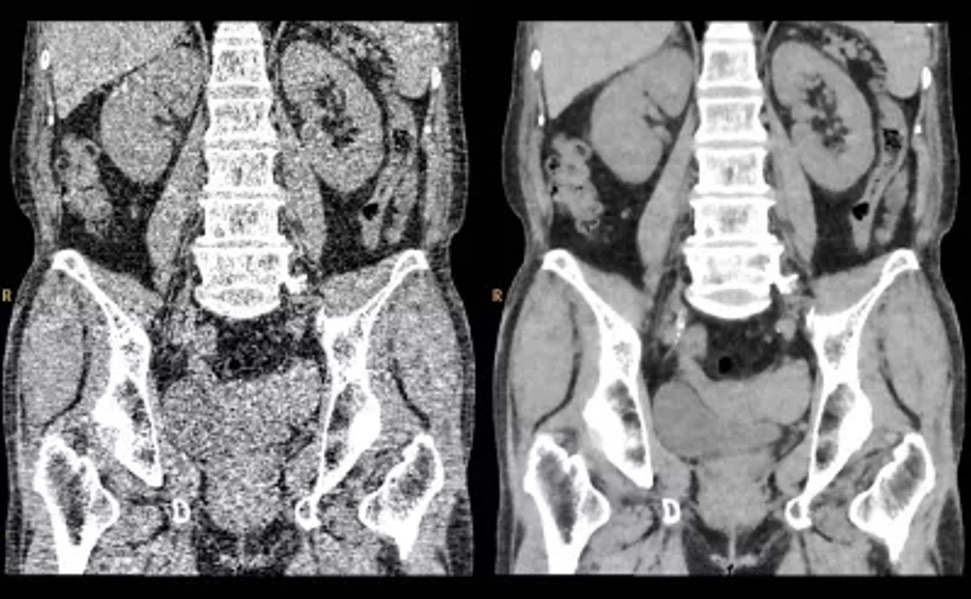
Figura 3. Restauración de una tomografía computarizada borrosa.

Pero el cálculo fraccionario no se detiene ahí. Zhang et al. (2020) han llevado las cosas un paso más allá, combinando el cálculo fraccionario con la inteligencia artificial para ayudar en la determinación de la muerte cerebral. Es como tener un detective matemático que puede ver patrones en las imágenes cerebrales que el ojo humano podría pasar por alto. Como explican Fatemi et al. (2021), las matemáticas como el CF puede adaptarse a diferentes tipos de imágenes y en diferentes partes del cuerpo.

Las matemáticas están permitiendo a médicos y científicos ver el cuerpo humano con mayor claridad. Están ayudando a detectar enfermedades en etapas tempranas para planificar tratamientos con mayor precisión y coadyuvar a entender mejor cómo funciona nuestro cuerpo.

La próxima vez que te hagas una radiografía o una resonancia magnética, recuerda que hay un poco de matemáticas trabajando detrás, ayudando a los médicos a ver lo que antes era invisible.

Este fascinante campo de estudio nos recuerda que las matemáticas no son sólo números en hojas, sino herramientas poderosas que pueden tener un impacto real y positivo en nuestras vidas o nuestra salud.

¿Cómo nos puede ayudar el cálculo fraccionario en la medicina?

Detección temprana de cáncer. El cáncer de mama es uno de los más comunes en mujeres, y la detección temprana es vital para un tratamiento efectivo. Investigadores han creado algoritmos basados en cálculo fraccionario que mejoran la calidad de las mamografías. Estos algoritmos permiten identificar microcalcificaciones, que son pequeños depósitos de calcio que pueden ser señales iniciales de cáncer, con mayor precisión que los métodos tradicionales.
Imágenes cerebrales más nítidas. En el estudio de enfermedades neurodegenerativas, como el Alzheimer, es crucial contar con imágenes cerebrales de alta calidad. El cálculo fraccionario se ha utilizado para mejorar la resolución de las imágenes por resonancia magnética del cerebro, facilitando la detección de cambios sutiles en su estructura que podrían indicar la enfermedad en etapas tempranas.
Mejora de las imágenes de ultrasonido. Las imágenes de ultrasonido son una herramienta diagnóstica común, especialmente en obstetricia, pero a menudo presentan un problema de ruido que las hace difíciles de interpretar. Técnicas basadas en cálculo fraccionario han sido aplicadas para reducir este ruido, resultando en imágenes más claras.
Análisis de la estructura ósea. La osteoporosis afecta la densidad y calidad de los huesos. Las técnicas de imagen tradicionales pueden tener dificultades para capturar la estructura porosa y fractal de los huesos. El cálculo fraccionario ha permitido desarrollar nuevos métodos de análisis de imágenes que evalúan mejor la calidad ósea, mejorando así los diagnósticos y tratamientos.
Mejora de las imágenes de tomografía computarizada. La tomografía computarizada es una técnica de imagen muy utilizada que produce imágenes tridimensionales del interior del cuerpo. Investigadores han aplicado el cálculo fraccionario para crear nuevos algoritmos de reconstrucción de imágenes de TC, logrando imágenes de alta calidad.

Figura 4. Diferentes imágenes médicas en las que se pudo mejorar la claridad, nitidez y eliminar el ruido.

¿Cuáles serían las dificultades que nos enfrentamos al trabajar con cálculo fraccionario?

Complejidad computacional. Los algoritmos basados en cálculo fraccionario suelen requerir una gran capacidad de procesamiento. Los investigadores están desarrollando métodos más eficientes y explorando tecnologías avanzadas, como el cómputo en la nube o cómputo paralelo, para superar estas limitaciones.
Interpretación de resultados. Aunque el cálculo fraccionario puede descubrir características sutiles en las imágenes médicas, interpretar estos resultados puede ser complicado. Se necesita más investigación para comprender plenamente cómo estas características se relacionan con los procesos biológicos subyacentes.
Estandarización. Para que estas técnicas sean adoptadas de manera amplia en la práctica clínica, es necesario establecer estándares y protocolos claros. Esto requiere una colaboración estrecha entre matemáticos, ingenieros y médicos.
Educación y formación. La introducción de estas técnicas avanzadas en la práctica médica requerirá programas de educación y formación específicos para los profesionales de la salud. Esto implica el reto de enseñar conceptos matemáticos complejos de una manera accesible y relevante para los médicos.

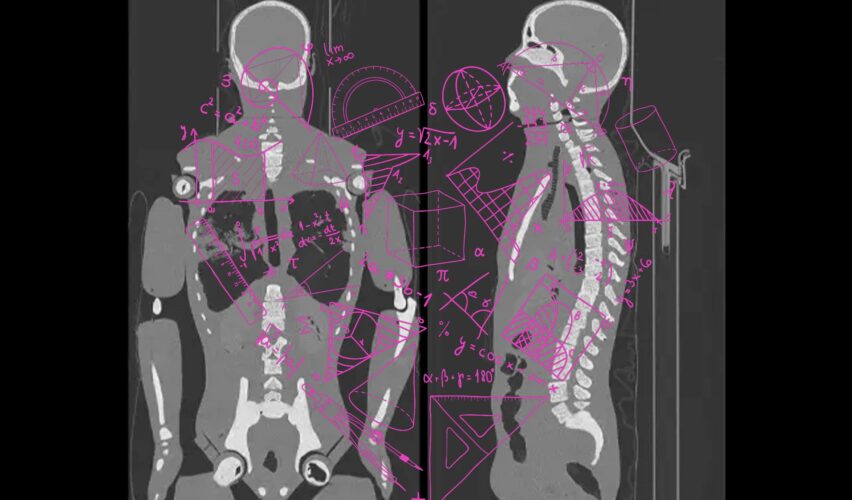
Figura 5. Imagen médica original (izquierda) e imagen médica procesada con cálculo fraccionario (derecha).

El cálculo fraccionario está revolucionando el campo de las imágenes médicas, ofreciendo nuevas formas de visualizar y comprender el cuerpo humano. Desde la detección temprana del cáncer hasta el estudio de la función cerebral, estas técnicas matemáticas avanzadas están abriendo posibilidades en el diagnóstico y tratamiento de enfermedades. A medida que seguimos explorando el potencial del cálculo fraccionario en las imágenes médicas, es emocionante pensar en las futuras consecuencias útiles.

Si estás interesado en conocer más en torno al cálculo fraccionario y sus aplicaciones, puedes visitarnos en los siguientes enlaces:

Referencias

Cha, S. (2006). Update on brain tumor imaging: from anatomy to physiology. American Journal of Neuroradiology, 27(3), 475-487.
Fatemi, M., Amiri, M., & Samavi, S. (2021). Fractal-based image enhancement using fractional calculus. IET Image Processing, 15(6), 1279-1291.
Gould, M. K., Maclean, C. C., Kuschner, W. G., Rydzak, C. E., & Owens, D. K. (2001). Accuracy of positron emission tomography for diagnosis of pulmonary nodules and mass lesions: a meta-analysis. Jama, 285(7), 914-924.
Huang, L., Ran, M., & Jiang, X. (2019). Fractional-order total variation image restoration based on primal-dual algorithm. IEEE Transactions on Image Processing, 28(5), 2303-2315.
Macías-Díaz, J. E. (2022). Fractional Calculus—Theory and Applications. Axioms, 11(2), 43.
Smith-Bindman, R., Miglioretti, D. L., & Larson, E. B. (2008). Rising use of diagnostic medical imaging in a large integrated health system. Health affairs, 27(6), 1491-1502.
Yin, C., Chen, Y., & Stark, S. M. (2020). Fractional-order derivative based bilateral filter for medical image denoising. Biomedical Signal Processing and Control, 60, 101967.
Zhang, Y., Wen, C., Zhang, Y., & Soh, Y. C. (2020). Determination of brain death using a novel deep learning approach based on fractional calculus. IEEE Transactions on Biomedical Engineering, 67(9), 2646-2656.